42
67
Spécial « infrasons »
Fig. 3 : Spectre d’isolement brut (différence entre niveau
sonore à l’extérieur et à l’intérieur) aux bruits
aériens extérieurs de basse fréquence. La valeur est
dépassée par 80 % des habitations danoises [11]
L’excitation se transmet préférentiellement aux vitrages et
aux planchers légers, mais elle peut aussi faire vibrer des
éléments du mobilier. Il est établi qu’une excitation pure-
ment aérienne suffit à mettre en vibration des vitrages.
Pour les planchers, Leventhall observe des résonances
dans les tiers d’octave 12,5 et 16 Hz, pour les vitrages,
dans le tiers d’octave 50 Hz [9].
Bien que les amplitudes soient en général trop faibles pour
endommager l’audition, ces manifestations sont souvent
très gênantes pour les occupants des logements touchés,
car les vibrations sont souvent associées à un endomma-
gement et à la dépréciation des biens.
A la lumière de ces éléments, il est clair que les problè-
mes de nuisances dans les basses fréquences doivent
être traités à la source et qu’il importe de mieux connaî-
tre l’émission des véhicules dans cette partie du spectre.
Le chapitre suivant aborde cet aspect.
Emission sonore routière à basse fréquence
Les informations disponibles dans la littérature sont plutôt
rares. La méthode en vigueur en France définit deux spectres
constants normalisés de telle sorte que leur niveau global
soit égal à 0 dB (A), selon que le trafic s’écoule sur un revê-
tement drainant ou non [12]. Dans les deux cas, la fréquence
minimale couverte est le tiers d’octave 100 Hz. Ceci n’a rien
d’étonnant puisque cette méthode s’appuie sur les résultats
de mesurage de bruit de roulement au passage.
La seule référence trouvée qui fournisse des spectres
jusqu’à des fréquences de l’ordre de 1 Hz est [9]. Toutefois,
elle s’appuie pour l’essentiel sur des travaux qui remon-
tent aux années 1970.
Le spectre de trafic routier défini dans la norme EN 1793-3
[13] «descend» jusqu’au tiers d’octave 50 Hz. Dans leur
ouvrage sur le bruit de contact pneumatique/chaussée,
Sandberg et Ejsmont affirment que ce spectre est censé
représenter un trafic urbain autour de 50 km/h et que
pour des vitesses plus élevées, il surestime largement les
basses fréquences [14]. Dans la même référence, on trouve
des spectres mesurés en 1982-84 et 1995-96 par l’insti-
tut suédois VTI, ainsi que des données japonaises, sans
autre précision d’origine. Tous ces spectres «commencent»
à 50 Hz. De nombreux autres spectres surgissent au fil
des pages de [14], et il semble que l’ouvrage n’en fasse
pas tout à fait la synthèse dans le sous-chapitre prévu à
cet effet. En outre, certains graphiques de [14] sont trop
peu lisibles pour être exploitables.
La référence [14] donne aussi une estimation de l’impact de
l’humidité de la chaussée sur le niveau de bruit au passage.
Alors que l’augmentation de niveau sonore est nette pour les
fréquences supérieures à 1 kHz, il n’y a pas de différence
significative entre la mesure sur chaussée sèche et celle
sur chaussée mouillée dans le cas qui nous intéresse.
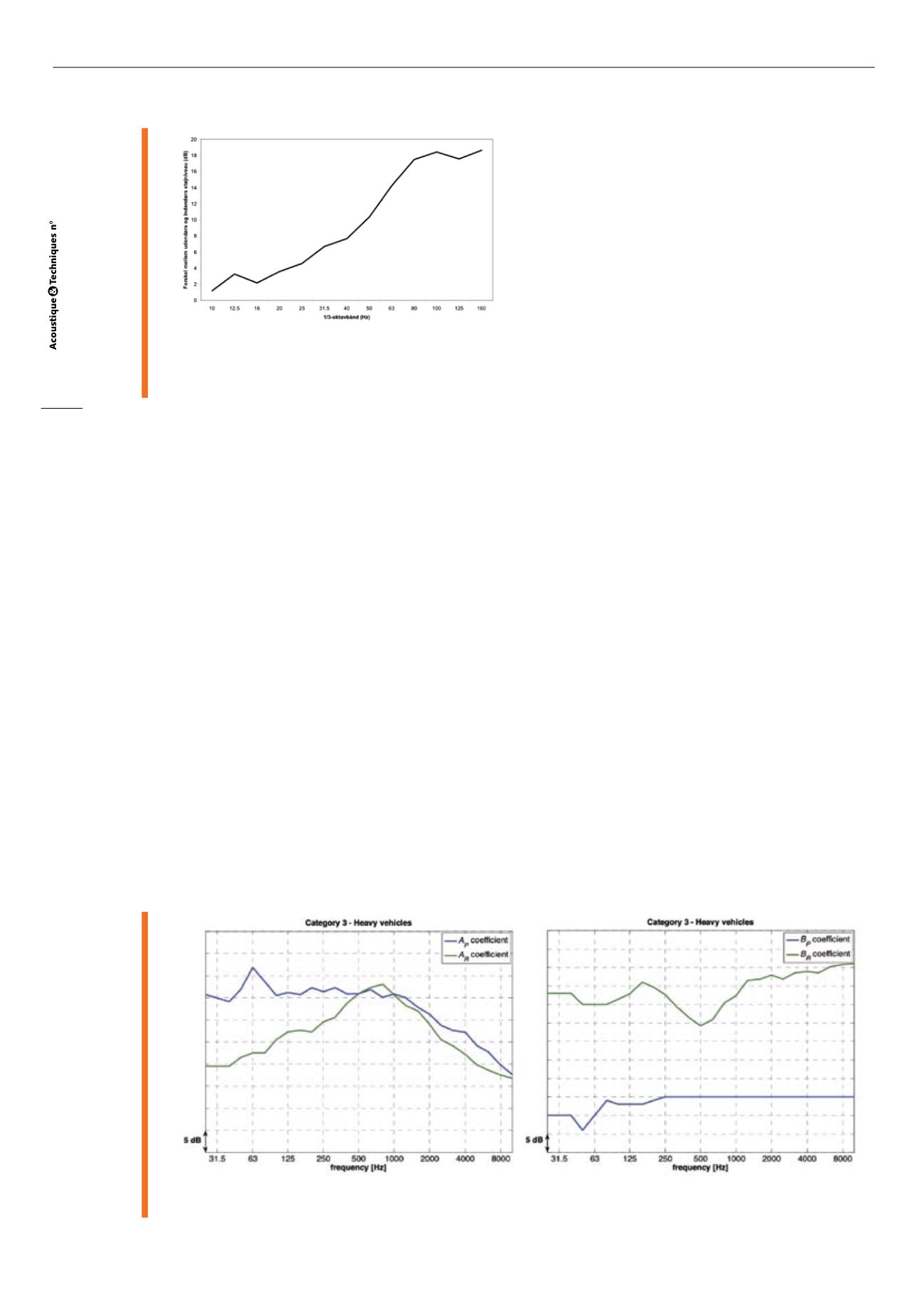
Le livrable 11 du projet européen IMAGINE formule un
modèle pour les tiers d’octave 25 à 10 000 Hz [15]. Comme
le modèle français, ce modèle distingue une composante
roulement et une composante propulsion, à la différence
près que ces composantes sont dépendantes du tiers
d’octave considéré (figure 4). Pour quatre catégories de
véhicules – véhicules légers, petits poids lourds, gros
poids lourds, 2-roues motorisés -, il contient des graphi-
ques représentant les spectres des quatre coefficients
principaux qui donnent l’ordonnée à l’origine et la pente
de chaque loi. Malheureusement, les graphiques en ques-
tion ne sont pas gradués de façon absolue en ordonnée.
La seule information disponible est que l’écart entre 2
graduations consécutives est de 5 dB. Pour les catégo-
ries véhicule léger et poids lourds, les spectres indiquent
que le bruit moteur domine à basse fréquence. On peut
s’interroger sur les fluctuations brutales qui apparaissent
sur ces spectres. Il est vrai que l’étendue de la base expé-
rimentale de ce modèle n’est pas connue.
Fig. 4 : Coefficients du modèle IMAGINE pour les poids lourds, en valeurs relatives. LwR=AR + BR
log(v/vref) et LwP=AP + BP x (v-vref)/vref. P pour propulsion, R pour roulement [15]


