38
67
Spécial « infrasons »
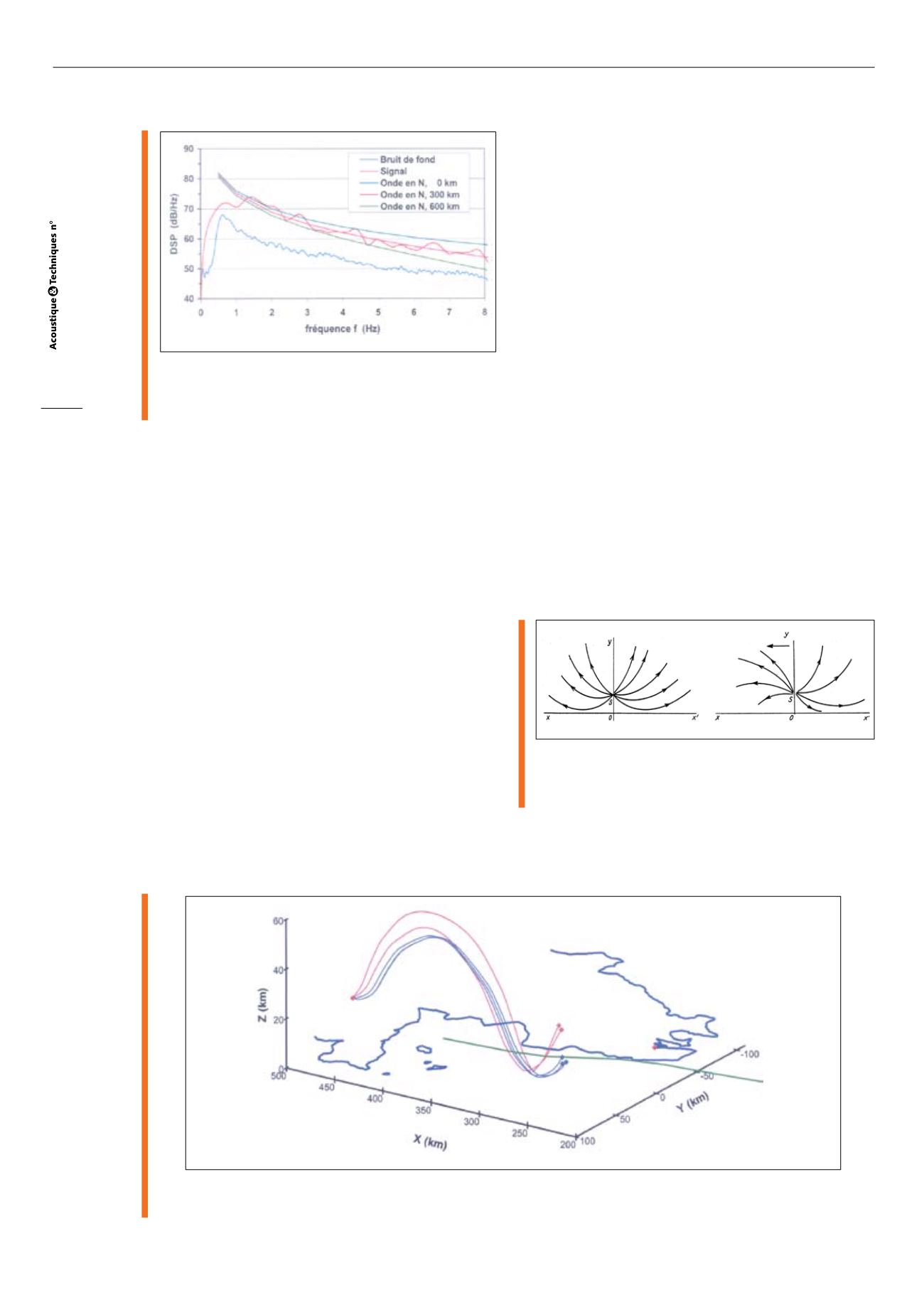
Fig. 10 : Spectres du bruit de fond et du signal, analyse en
distance. Extrait de la Réf. [4]
Background noise and signal spectra,
estimation of the distance. From Ref. [4]
Pour résoudre complètement le problème inverse, il faut
pouvoir estimer la distance curviligne parcourue dans
l’atmosphère par le train d’ondes. La figure 10 montre
le spectre du bruit de fond moyenné entre les différents
capteurs sur une durée de plusieurs minutes et le spec-
tre du signal moyenné sur la durée de l’arrivée principale.
Comme on le voit, le rapport signal sur bruit est très favo-
rable et on peut considérer la courbe rouge comme un
signal pur, du moins au-dessus de 1 Hz.
La méthode élaborée, présentée dans la référence [8], se
base sur l’hypothèse que le spectre du bang sonique initial
doit se retrouver dans un signal formé d’échos multiples,
du moins en ce qui concerne sa pente (il est clair qu’aucune
arche n’est plus visible au-delà d’une certaine distance de
propagation). La pente initiale de l’enveloppe de l’onde
en N est au départ de − 6 dB par octave comme le montre
la figure 4 gauche, mais elle augmente en cours de propa-
gation sous l’action de l’absorption atmosphérique d’une
part, de la dissipation des effets non-linéaires d’autre part.
On peut ainsi déterminer la pente de l’enveloppe et par
extension celle du spectre du signal à différentes distan-
ces, en faisant l’hypothèse d’un trajet stratosphérique.
On a ainsi estimé que la distance de propagation la plus
probable pour le signal reçu à Flers était de l’ordre de
300 km, comme le suggère la figure 10 où sont repré-
sentées les enveloppes théoriques du spectre de l’onde
en N à 0, 300 et 600 km.
En définitive, il apparaît possible de tirer à partir de la
station de Flers des rayons inverses en vue d’intercepter
la trajectoire du vol “Concorde” Air France New York-Paris
AF002 dont les données ont été recalculées par l’APCOS
[5] en fonction de la météorologie du jour issue des radio-
sondages de la station de Brest.
Notons que l’inversion des trajectoires de rayons sono-
res pose un problème particulier, ces trajectoires n’étant
pas réversibles en présence d’un gradient de vent car
leur concavité change selon que l’on se trouve au vent ou
sous le vent (figure 11 droite), ce qui n’est pas le cas en
présence d’un gradient de température (figure 11 gauche).
Cette contradiction apparente du principe de Fermat et
du théorème de réciprocité est examinée dans la réfé-
rence [9] mais pose un problème numérique insurmonta-
ble, à moins d’inverser de façon artificielle le sens du vent
à toutes les altitudes.
Fig. 11 : Effets acoustiques de gradients de température
et de vent. Extrait de la Réf. [9]
Acoustic effects of a temperature gradient
and a wind gradient. From Ref. [9]
Fig. 12 : Calcul de rayons inverses issus de la station de Flers. Extrait de la Réf. [4]
Calculation of reverse rays coming from the station at Flers. From Ref. [4]


