37
67
Spécial « infrasons »
Stations Azimut de
réception
Horaire
d’émission
Longueur
orthodromique
Horaire
de réception
c sol
expérimentale
Lycksele 258,5° 20h11min52s 3042 km 2h59min 25s 302,6 m/s
Jämton
250° 20h30min05s 2835 km 23h09min00s 297,3 m/s
Kiruna
243° 20h30min57s 2812 km 23h07min40s 299,1 m/s
Kiruna
251,5° 20h17min10s 3085 km 23h07min25s 302,0 m/s
Stations Azimut de
réception
Horaire
d’émission
Temps de
propagation
Horaire
de réception
c sol
calculée
Lycksele 256,16° 20h13min15s 2h46min10s 22h59min25s 302,6m/s
Jämton 248,3° 20h29min54s 2h39min06s 23h09min00s 300,5m/s
Kiruna
240,6° 20h30min17s 2h37min23s 23h07min40s 300,6m/s
Kiruna
249,8° 20h16min40s 2h50min45s 23h07min25s 300,4m/s
Tabl. 1: Vol BA002, données réelles (en haut) et calculées (en bas).
Extrait de la Réf. [4]
Flight BA002, real data (above) and
calculated data (below).From Ref. [4]
Il est évidemment difficile de valider ces calculs de façon
formelle. Toutefois, un certain nombre de données expéri-
mentales et de données calculées à l’aide du code SIMOUN
peuvent être comparées. Dans le tableau 1 (en haut), on
a supposé que le “Concorde” était passé à l’heure prévue
par le plan de vol pour calculer une vitesse de propagation
projetée au niveau de la mer à partir de l’horaire d’arrivée
du train d’ondes sous l’azimut enregistré. La position de
l’avion et la distance ont été calculées par intersection de
la trajectoire théorique et de l’orthodromie (arc de grand
cercle) tirée de la station d’écoute selon l’azimut opposé.
En bas, on a fait figurer les résultats issus du calcul de
rayons 3D, avec un recalage artificiel des instants d’arri-
vée. La bonne concordance des azimuts de réception et
des vitesses de propagation projetées milite en faveur
des hypothèses faites et prouve notamment que le vol de
la British Airways est bien à l’origine des signaux enregis-
trés par les trois stations.
Analyse des signaux infrasonores
L’analyse spatio-temporelle des signaux enregistrés four-
nit des renseignements intéressants qui, comme on l’a
vu, peuvent être exploités soit via la météorologie réelle,
soit via une météorologie statistique, ou même sans en
tenir compte en première approximation (trajets ortho-
dromiques).
Sachant que les stations d’enregistrement du CEA compor-
tent plusieurs capteurs microbarographes répartis sur
le terrain, on peut par ailleurs appliquer une technique
classique de goniométrie basée sur les intercorrélations
temporelles entre capteurs pour déterminer la direction
de provenance moyenne du signal. La méthode dévelop-
pée à l’Onera consiste à trouver les temps de corréla-
tion entre capteurs, puis à déterminer par itération en
azimut la direction de provenance et la vitesse de propa-
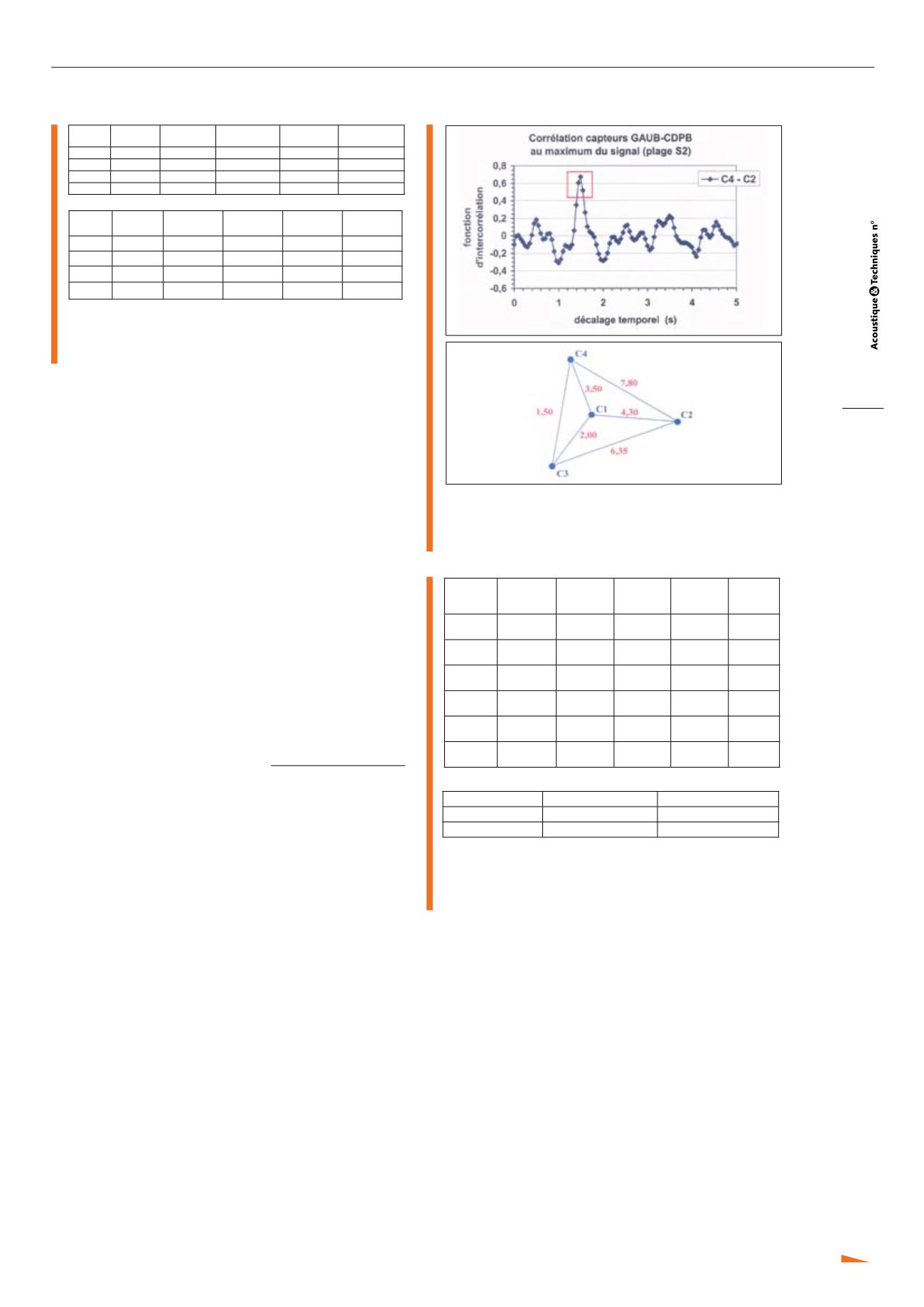
gation apparente des trains d’ondes. La figure 9 gauche
montre la fonction de corrélation entre deux capteurs
qui est obtenue en faisant glisser un signal sur l’autre,
la durée de signal considérée étant de 12 s (tranche S2
de la figure 6). Le maximum correspond à la meilleure
concordance qui donne le temps de propagation entre les
deux capteurs. Un examen à l’œil nu de la figure 9 droite
qui représente le réseau de la station de Flers et indique
les temps de propagation entre capteurs permet de voir,
en première analyse, que le train d’ondes provient de la
direction Ouest-Nord-Ouest.
Fig. 9 : Calcul de corrélation, temps de propagation
entre capteurs. Extrait de la Réf. [4]
Correlation function, duration of propagation
between the sensors. From Ref. [4]
N° de
la plage
temporelle
Fenêtre
temporelle
Célérité
corrigée
Ecart-type Angle d’azi-
mut
Angle de
site
S1 22min00s
à 12 s
328,7 m/s 2,7 m/s
285,0°
0°
S2 22min12s
à 24s
334,3 m/s 0,9 m/s
285,8°
0°
S3 22min24s
à 36s
336,3 m/s 1,4 m/s
285,7°
1,3°
S4 23min12s
à 27s
343,3 m/s 2,8 m/s
284,9°
11,7°
S5 23min27s
à 47s
363,8 m/s 3,5 m/s
284,5°
22,5°
S6 25min55s
à 26min12s
429,9 m/s 5,5 m/s
289,3°
38,6°
S1 à S3
Azimut ± 0,5°
Site ± 2,0°
S4 et S5
Azimut ± 1,0°
Site ± 3,0°
S6
Azimut ± 3,0°
Site ± 6,0°
Tabl. 2 : Calcul goniométrique (en haut) et incertitudes (en bas).
Extrait de la Réf. [4]
Goniometric calculation (above), and uncertainties (below).
From Ref. [4]
La vitesse de propagation apparente (célérité du front d’onde
supposé plan) doit évidemment être la même entre chaque
paire de capteurs, un seul azimut d’arrivée permettant en
principe de satisfaire cette condition. En réalité, on déter-
mine l’azimut qui minimise l’écart constaté entre les célé-
rités relatives aux six paires considérées, d’où les écarts-
types indiqués dans le tableau 2. L’étape suivante consiste
à corriger la célérité moyenne constatée de la composante
utile de la vitesse du vent local pour pouvoir la comparer à
la vitesse du son ambiante et ainsi déterminer, par calcul
de cosinus, l’angle d’incidence du train d’ondes (ou angle
de site mesuré à partir de l’horizontale). On voit sur le
tableau 2 que l’arrivée principale de la figure 6 arrive sous
incidence rasante, l’incertitude en azimut étant d’environ
0,5°. La vitesse du son ambiante près du sol a été estimée
à 336 m/s d’après le bulletin météorologique local ALADIN
(données interpolées de Météo-France).


