42
68
Spécial « Congrès Acoustics 2012 »
Étude expérimentale d’égalisation modale d’une salle aux basses fréquences à l’aide d’absorbeurs électroacoustiques actifs
Une alternative à ces stratégies de contrôle d’impédance
est de remplacer le dispositif de contrôle actif par une
impédance électrique de synthèse [6]. Le courant circu-
lant dans la bobine du haut-parleur, et par conséquent
la force de réaction de la membrane à une perturbation
extérieure, est alors modulé en fonction de la force élec-
tromotrice générée à la sortie électrique du haut-parleur,
qui est liée à la vitesse vibratoire de la membrane. C’est
cette dernière configuration qui a été sélectionnée pour
la réalisation pratique.
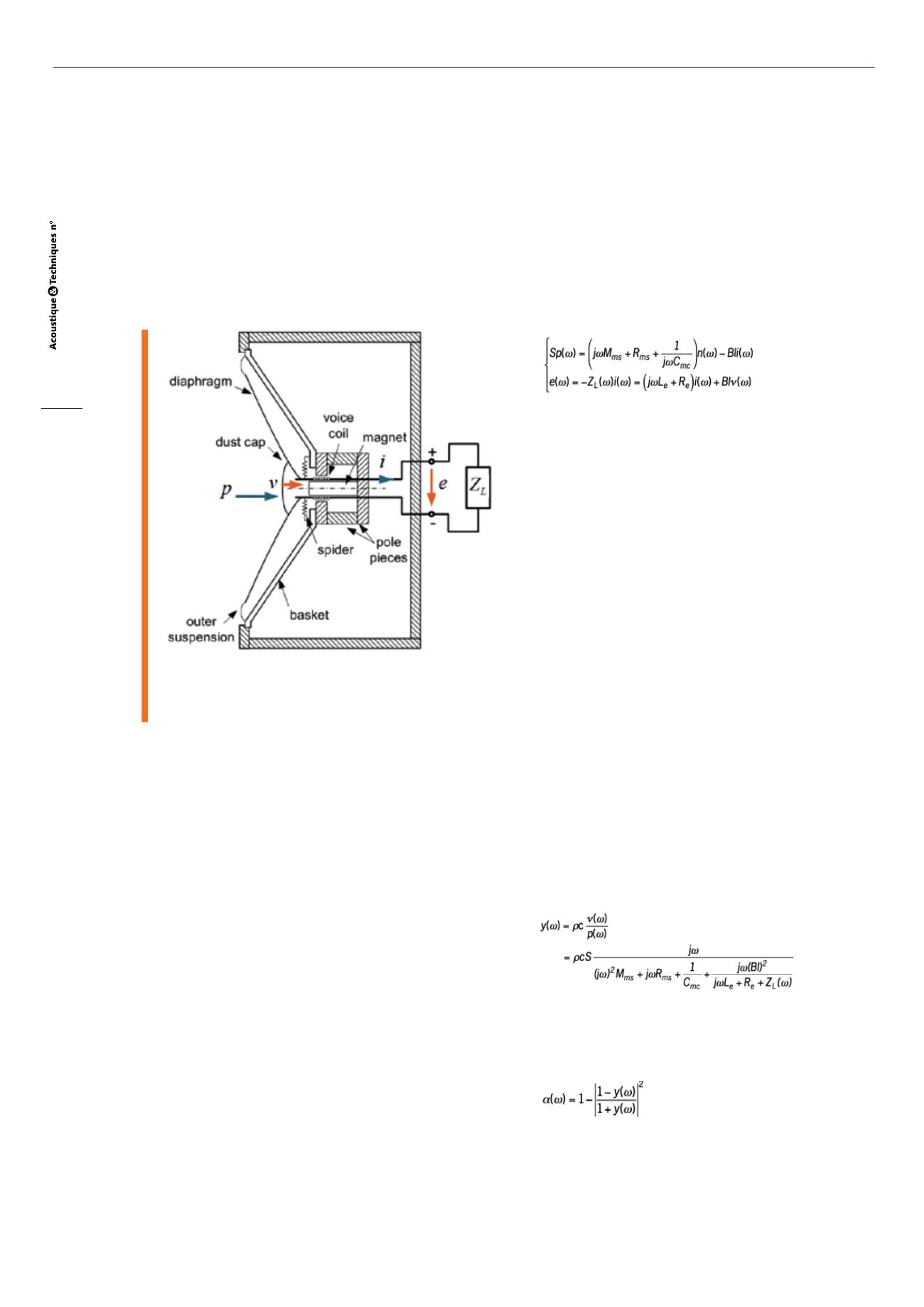
Fig. 2 : Schéma d’un haut-parleur en enceinte close connecté
à une charge électrique spécifique
Schematic of a direct-radiator loudspeaker system
when connected to an electrical load
Formulation
Dans ce qui suit, nous avons choisi de présenter un modèle
extrêmement simple d’un haut-parleur, permettant de
comprendre le fonctionnement général. En particulier,
il est fait ici l’hypothèse que les variations des quantités
acoustiques, et par conséquent électriques, mises en jeu
sont négligeables devant les valeurs statiques (hypothèses
de l’acoustique linéaire), et que le moteur du haut-parleur
reste linéaire dans ces conditions. Il est également fait
l’hypothèse que l’impédance mécanique de la membrane,
ainsi que les modifications de cette impédance par contrôle
semi-actif ou actif, est grande devant l’impédance de
rayonnement de la membrane mobile. Par conséquent,
il n’est pas nécessaire de tenir compte du rayonnement du
haut-parleur dans ce qui suit. Cette hypothèse peut être
remise en question, mais cela n’enlève rien de la généra-
lisation des discussions qui vont suivre.
Le haut-parleur électrodynamique à bobine mobile est un
système linéaire invariant, dont la dynamique peut être
exprimée principalement par deux équations couplées :
la loi de Newton du côté mécanique et la loi des mailles du
côté électrique. Considérons un haut-parleur dont l’équi-
page mobile est constitué d’une membrane suspendue sur
son pourtour par une suspension élastique et à sa base par
un spider. Cet ensemble est solidaire à sa base à un petit
cylindre autour duquel est enroulée une bobine de cuivre.
Celle-ci est susceptible de se déplacer selon un mouve-
ment axial le long de l’axe de symétrie du haut-parleur,
dans l’entrefer d’un aimant permanent entouré de pièces
polaires. Ce haut-parleur est inclus dans une enceinte
close de volume V
b
, et connecté à une charge électri-
que complexe de valeur Z
L
(
ω
) (
ω
désignant la pulsation
en régime harmonique), comme illustré sur la figure 2.
Il est aussi possible de modéliser la dynamique du haut-
parleur en utilisant ses paramètres en petits signaux [4],
permettant d’écrire un système d’équations, reliant les
accès acoustiques (pression p et vitesse vibratoire v) et
électriques (tension e et intensité i) du haut-parleur :
(1)
où M
ms
désigne la masse dynamique de l’équipage mobile,
R
ms
la résistance mécanique, et C
mc
=C
ms
C
mb
/(C
ms
+C
mb
)
la compliance mécanique (inverse de la raideur) équiva-
lente à la mise en série des suspensions du haut-parleur
(C
ms
) et de la suspension acoustique du volume de l’en-
ceinte (C
mb
=V
b
/
ρ
c
2
S
2
où
ρ
et c désignent la densité
de l’air et la célérité des ondes acoustiques dans l’air).
Du côté électrique, R
e
et L
e
désignent la résistance et
l’inductance électrique de la bobine. Enfin, S désigne la
surface effective de la membrane, et Bl le facteur de force
du transducteur électrodynamique.
Dans ce système d’équations, l’élément contrôlable est
bien évidemment l’impédance électrique de charge Z
L
(
ω
)
,
qui peut être vue comme un régulateur du courant circu-
lant dans la bobine, en fonction de la tension électrique
résultant de la mise en vibration de l’équipage mobile.
Ce courant étant directement relié à la force de Laplace
appliquée à la membrane, il en découle que cette impé-
dance de charge peut également être considérée comme
un régulateur de la vitesse vibratoire de la membrane en
fonction de la perturbation acoustique extérieure, expri-
mée comme une force de pression Sp.
Du système d’équations (1), il est assez aisé d’exprimer
l’admittance acoustique présentée par la membrane du
haut-parleur (normalisée à l’admittance caractéristique de
l’air), comme une fonction de transfert complexe :
(2)
Enfin, le coefficient d’absorption acoustique sous inci-
dence normale peut être directement dérivé de l’admit-
tance acoustique, selon l’expression :
(3)
Ce résultat indique que, en fonction de la valeur ou de l’allure
de l’admittance acoustique que l’on dispose en charge du haut-
parleur, il est possible de varier le coefficient d’absorption
acoustique, au moins autour de la résonance du haut-parleur,
qui est en général de l’ordre de quelques dizaines de Hertz.


