51
68
Spécial « Congrès Acoustics 2012 »
Modélisation de la propagation acoustique en milieu extérieur par une approche temporelle : validation expérimentale sur site
Une série de trois tirs a été effectuée. La directivité de
la source n’a pas été mesurée et on supposera que celle-
ci est monopôlaire. La puissance de la source S
exp
(ƒ)
peut alors être calculée à partir des formes d’onde. Pour
cela, on considère la forme d’onde à x = 7,5 m ; la forme
d’onde de l’onde directe peut alors être obtenue en fenê-
trant le signal.
Dans le domaine fréquentiel, l’onde directe p
D
peut s’écrire
comme le produit de la fonction de Green en champ libre
et de la puissance de la source :
(1)
où
ω
=2
π
ƒ est la pulsation, R la distance source-récepteur
et avec k
eff
=
ω
/c
eff
. Le terme ceff correspond à la célérité
effective du son. La partie correspondant à l’onde directe
d’une forme d’onde obtenue expérimentalement est repré-
sentée sur la figure 5. La puissance de la source corres-
pondante est tracée en fonction de la fréquence sur la
figure 6. La puissance de la source obtenue agit comme
un filtre passe-bande. Le maximum de celle-ci est atteint à
une fréquence proche de 900 Hz. On peut aussi noter que
le contenu fréquentiel de la source est important jusqu’à
10 kHz environ. Dans la suite, les comparaisons ne seront
effectuées que jusqu’à une fréquence de 3 kHz.
Fig. 6 : Puissance de la source en fonction de la fréquence
obtenue (en ligne rouge) à partir de la forme d’onde
expérimentale et (en ligne noire) à partir de son
approximation
Source strength versus frequency. The black and red
lines correspond respectively to measurements and
to the approximation
Pendant la phase de décompression, la forme d’onde
présente quelques oscillations. Afin de ne pas prendre
en compte celles-ci, une approximation polynômiale par
morceaux de la forme d’onde est utilisée dans la suite
(voir Fig. 5 et 6) [7].
Comparaison avec des résultats d’une
simulation numérique
Description du modèle de propagation
Les équations d’Euler linéarisées sont résolues dans le
domaine temporel par des méthodes de type différences
finies, appelées FDTD pour Finite-Difference Time-Domain.
La condition limite d’impédance est implémentée à l’aide
d’une technique de convolution récursive [5].
La topographie est prise en compte en utilisant des coor-
données curvilignes [12,6]. Les différentes méthodes numé-
riques employées sont décrites en détail dans [5] et [13].
Puisque la géométrie est invariante dans la direction y, la
simulation numérique est réalisée pour une configuration
2-D. Les coordonnées curvilignes sont ici appelées (
ξ
,
η
).
Les équations de passage des coordonnées curvilignes
vers les coordonnées courantes s’écrivent :
(2)
où H est le profil du terrain, représenté en fonction de x sur
la figure 3. Le domaine de calcul contient 11 000 points
dans la direcion
ξ
et 1 501 points dans la direction
η
.
Le maillage est uniforme avec un pas spatial
Δξ
=
Δη
=
0,01 m. Le nombre CFL défini par CFL = c0
Δ
t/
Δ
x est fixé
à 0,5. Environ 22 000 itérations temporelles sont réali-
sées. Le calcul est effectué sur une machine vectorielle
NEC SX-8 et nécessite 8 heures CPU.
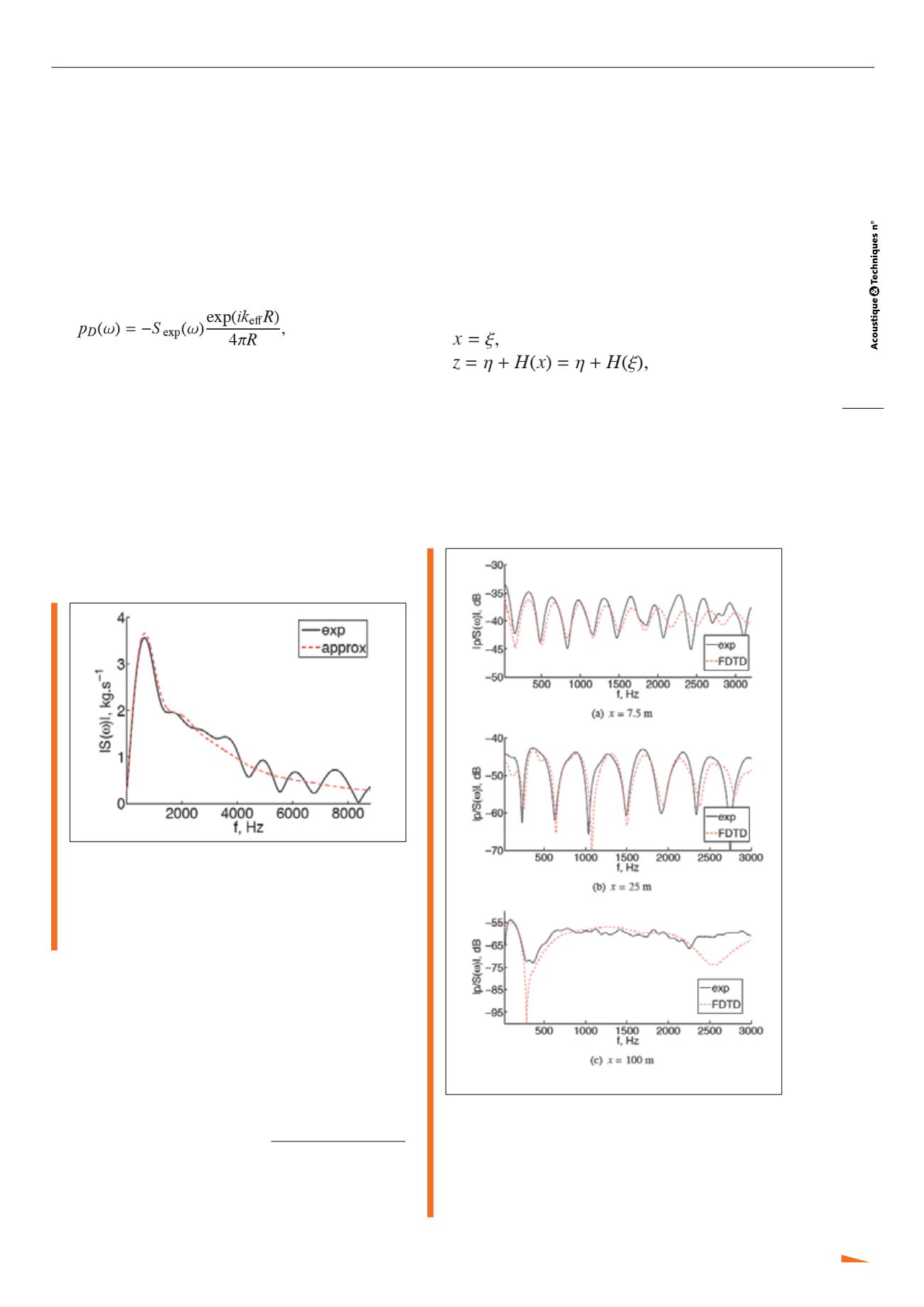
Fig. 7 : Niveaux de pression normalisés par la puissance de la
source pour les récepteurs situés en (a) x = 7,5 m,
(b) x = 25 m et (c) x = 100 m. La hauteur de la source est
z
S
= 1m.
–
mesure et
- -
simulation
Sound pressure levels normalized by the source strength
at receivers located at (a) x = 7.5 m, (b) x = 25 m
and (c) x = 100 m. The height of the source
is z
S
= 1 m.
–
experiment and
- -
FDTD


