16
65
2
e
trimestre 2011
Nouvelle méthode de mesure du coefficient de diffusion acoustique des parois à relief dans les locaux industriels
Afin de pouvoir déterminer à terme le coefficient de diffusion
des parois à relief présentes dans les locaux industriels,
nous avons choisi dans ce travail d’adapter la méthode
de mesure de Vorländer et Mommertz à des milieux confi-
nés réverbérants bruyants. Pour cela, nous avons utilisé
une antenne acoustique à directivité constante en fonc-
tion de la fréquence [7] comme récepteur et une source
impulsionnelle [8]. Notre travail porte sur la validation
expérimentale de cette technique sur un échantillon de
paroi ondulée.
Méthode de mesure du coefficient de diffusion
acoustique en champ libre
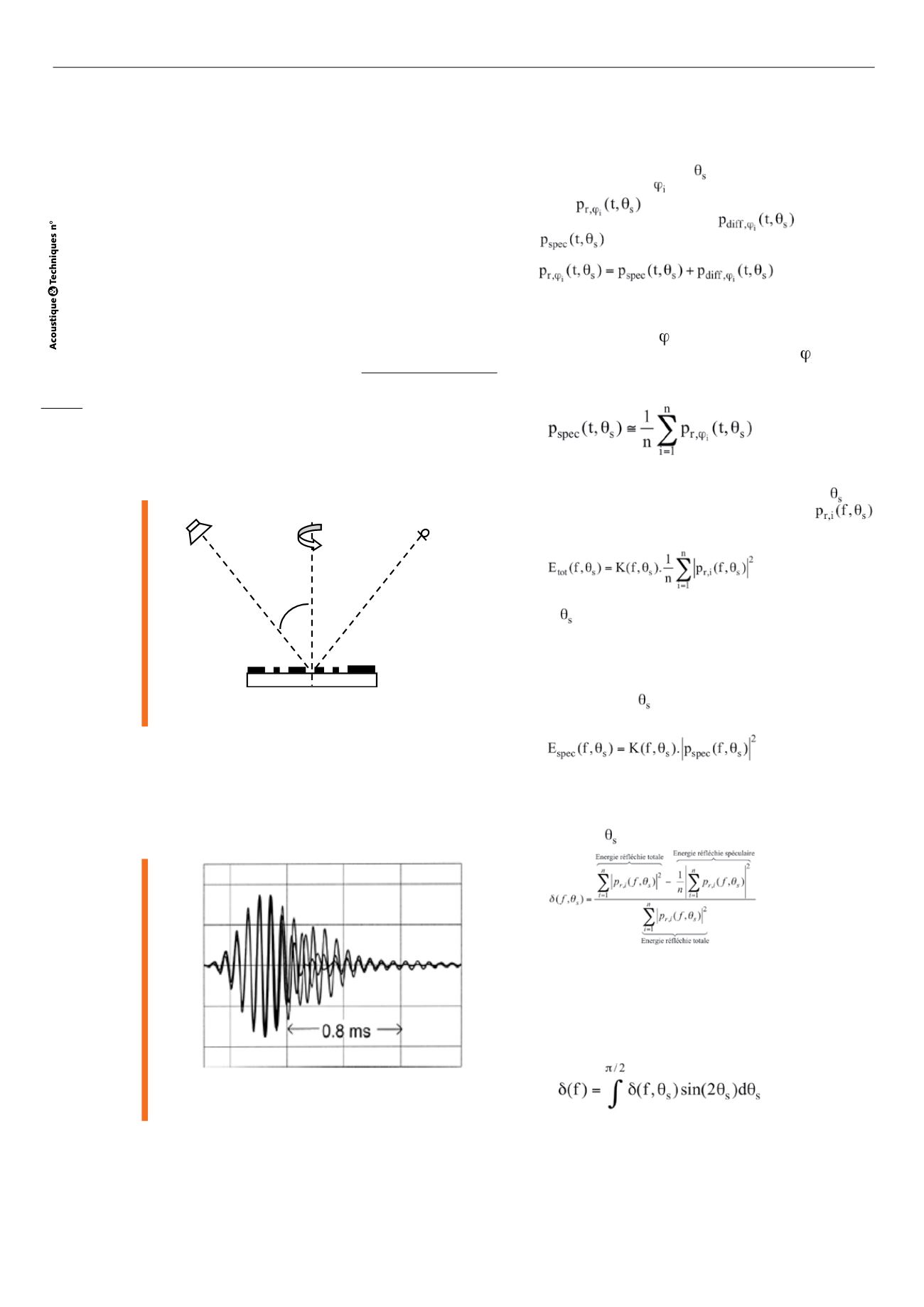
La source (haut-parleur) et le récepteur (microphone) sont
placés en champ lointain positionnés dans la direction
spéculaire. On retrouve une plaque tournante sur laquelle
est placé l’échantillon à relief étudié qui permet d’effectuer
des mesures pour de multiples orientations.
s
Paroi à relief étudiée
Fig. 2 : Principe de la méthode de détermination du
coefficient de diffusion en champ libre [6]
La figure 3 montre un exemple d’impulsions réfléchies
obtenues pour trois orientations de la surface diffuse.
Le signal incident est un burst centré sur le 1/3 d’oc-
tave 10 kHz.
Temps
Pression acoustique (Pa)
Fig. 3 : Impulsions réfléchies pour 3 orientations
différentes d’une paroi à relief [6]
On constate sur cette figure que la partie initiale des répon-
ses impulsionnelles sont cohérentes (en phase) tandis que
le reste de l’évolution temporelle montre que ces mêmes
impulsions ne sont plus en phase.
Cette deuxième partie de chaque réponse impulsion-
nelle est donc attribuée à la composante non spéculaire.
Pour un angle d’incidence de la source et du récepteur
et une orientation , les pressions acoustiques réflé-
chies
peuvent s’écrire comme la superposi-
tion d’une composante diffuse
et spéculaire
:
(2)
La pression acoustique spéculaire est obtenue en moyen-
nant un nombre important de pressions acoustiques réflé-
chies suivant l’angle : on considère que la composante
spéculaire reste cohérente en fonction de contraire-
ment à la composante diffuse qui, une fois moyennée,
s’atténue :
(3)
Dans les conditions de champ lointain, l’énergie totale
réfléchie moyennée dans la direction spéculaire peut
s’écrire en fonction des transformées de Fourier
des pressions acoustiques temporelles mesurées :
(4)
K(f, ) est une constante dépendante de la puissance
acoustique de la source ainsi que des positions géomé-
triques de la source et du récepteur. L’énergie réfléchie
spéculaire est également proportionnelle au module au
carré de la transformée de Fourier de la pression acous-
tique spéculaire :
(5)
En combinant les équations (3), (4) et (5), on obtient un
coefficient de diffusion acoustique dans une direction
spéculaire :
(6)
avec n >> 1
A partir de ces différents coefficients de diffusion, il est
possible de déduire le coefficient de diffusion pour une
incidence aléatoire :
(7)
Afin de pouvoir utiliser cette méthode de mesure dans des
conditions acoustiques défavorables comme celles des
ateliers de travail (conditions semi-réverbérantes avec
présences de sources pouvant être très bruyantes), nous
avons remplacé le microphone récepteur par une antenne
directive et la source par une source impulsionnelle.
Haut parleur
Microphone


