Version HTML de base

58
Fig. 3 : Graphes des régimes moteur en fonction de la vitesse
et du rapport de boîte de la moto catégorie 5
Tous ces paramètres relatifs aux conditions de mesure
permettent d’envisager une modélisation de la puissance
acoustique des deux-roues.
Modélisation
L’analyse a été réalisée à partir de la puissance acoustique
calculée en chaque point de mesure selon l’équation (2).
L
wA
= L
mesuré
- K
2
+ 10log
10
2
π
r
2
(2)
avec :
L
wA
: puissance acoustique en dBA
K
2
: coefficient d’environnement en chaque point en dBA
r : distance entre la moto et le point de mesure en mètres
Les variables influentes ont été déterminées à partir d’une
analyse en composantes principales avec comme facteurs :
le L
w
A, le régime moteur divisé par 1000, le logarithme
décimal de la vitesse, l’allure et le sens de passage de la
moto. Le tracé des valeurs propres permet de retenir 3
facteurs influents. La projection sur le premier plan facto-
riel permet de faire les remarques suivantes :
- L
wA
est corrélé avec log
10
(V) et le régime/1000,
- Log
10
(V) et régime/1000 sont fortement corrélés,
- Log
10
(V) et l’allure sont indépendants.
À partir de cette analyse en composantes principales [6]
[7], on élabore un modèle en prenant en compte le L
w
A
en fonction du log
10
(V) et on sépare l’allure stabilisée de
l’allure accélérée.
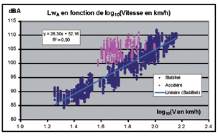
Fig. 4 : Graphe de Lw
A
en fonction de log
10
(V)
Modélisation en allure stabilisée
On trace le L
wA
en fonction du logarithme décimal de la
vitesse pour l’ensemble des points de mesure (figure 4).
Pour chaque motocyclette, les régressions obtenues en
logarithme décimal de la vitesse ont un coefficient de
détermination R
2
≥
0,9. En première approche, la pente
et l’ordonnée à l’origine semblent varier en fonction du
nombre de cylindres. Par ailleurs, il semble possible de
faire une séparation entre les motos récentes avec pot
catalytique et celles plus anciennes avec un pot d’échap-
pement normal.
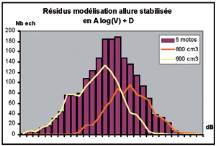
À partir de cette modélisation de l’ensemble des motos,
on trace le diagramme des résidus en ajoutant une distinc-
tion suivant la cylindrée (figure 5).
La courbe des résidus pour l’ensemble des motos est
proche d’une gaussienne. La distinction suivant la cylin-
drée fait apparaître deux populations décalées d’environ
2 dB(A).
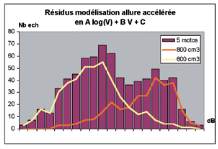
Modélisation en allure accélérée
Pour l’allure accélérée, on fait l’hypothèse que la puissance
acoustique en allure accélérée est la somme de la modéli-
sation de l’allure stabilisée et d’un écart entre l’allure accé-
lérée et l’allure stabilisée. On obtient ainsi une modélisa-
tion de l’allure accélérée de la forme suivante (3).
L
wA
= A log
10
(V) + BxV+ C
(3)
Emission acoustique des deux-roues motorisés / 2
e
partie : Les motocyclettes
Fig. 5 : Diagramme des résidus pour l’allure stabilisée
Fig. 6 : Diagramme des résidus pour l’allure accélérée

