Version HTML de base

49
supposed that all these variables are independent and quan-
tifiable, the dynamic stresses can be expressed as:
σ
dyn
= F (A, M, S,
ξ
,
θ
, f)
(5)
In this study, a model, based on a single degree of freedom
(1 dof) system was applied for modelling the human body
exposed to mechanical vibrations. By assuming that the exci-
tation produces a vibration at the natural frequency (f = f
n
)
as drivers are usually exposed to random or transient excita-
tions, a simplified model for computing the dynamic stresses
has been developed from the transmitted force formulation by
considering the bodymorphology (mass M and cross sectional
area at the intervertebral disc S) and the posture angle
θ
:
where:
(6)
A the applied acceleration amplitude to the seat; B is a
variable; S the average cross-section of disc;
θ
the posture
angle and;
ξ
the damping rate; M the body weight.
Using the FE model of the rachis, L1-L5, the dynamic
stresses observed on level L4-L5 were recorded. The anal-
ysis shows that for an intermediate body (body weight of
75 kg, intermediate posture
θ
=15°; an intermediate bone
structure S=1700mm
2
and a damping rate of 30%) the
model of prediction of the dynamic stresses becomes:
σ
dyn
= 0.06 A (MPa) with R
2
=96,5%
(7)
Fatigue analysis
Failure modes
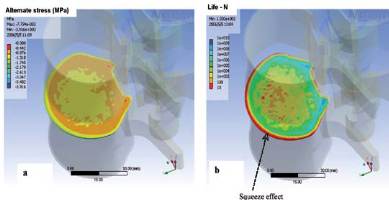
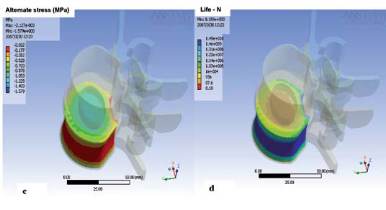
Numerical simulations have been conducted on the units
L4-L5 in order to predict the fatigue behaviour of vertebrae
of lumbar spine. Failures modes were analyzed. Figure 5
shows the stresses and number of cycles to failure on the
endplates (Fig 5 a, b) and on L5 vertebra (Fig. 5c, d) under
a cyclic loading equal to 60% of the ultimate load.
Accordingly to Brinckman studies [13], three modes of
fractures can be identified:
- Stellate fracture of endplate : two or more cracks running
from the centre towards the periphery of the endplate
(figure 5 a, b and e) ;
- Disc intrusion : intrusion of the disc material into the
trabecular bone observed in combination with some of
the above fractures types(figure 5c, d and e)
Fig. 5 (a), (b), (c), (d) : Failure modes for applied stresses of 60% the ultimate stress

