Version HTML de base
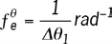
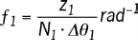
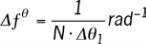
19
Mesure haute précision de vitesse angulaire instantanée pour la surveillance et la caractérisation d’excitation en machine tournante
le traitement du signal postérieur. Ainsi, l’échantillonnage
angulaire permet de localiser précisément les harmoni-
ques relatifs au passage d’une géométrie discrète tour-
nant à une vitesse quelconque. Ce paragraphe démontre
les conditions requises et met en évidence cette propriété
sur un exemple précis de caractérisation de l’excitation
par l’Erreur de Transmission.
Notion de fréquence angulaire
L’échantillonnage angulaire conduit naturellement à la
notion de fréquence angulaire ou de longueur d’onde
angulaire qui est fortement reliée au caractère discret
des éléments mécaniques généralement utilisés dans
les transmissions de puissance (engrenages, courroies
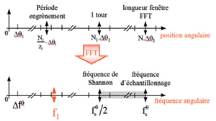
synchrones, chaînes, ...). La figure 7 illustre les grandeurs
caractéristiques d’un signal échantillonné angulairement
et de sa Transformée de Fourier Discrète (TFD) pour une
géométrie discrète tournante présentant z
1
éléments (par
exemple, le nombre de dents d’un engrenage).
Toutes les périodes représentatives y sont portées, en
particulier :
- la longueur du pas d’échantillonnage
∆
θ
1
, qui est donnée
par la précision du codeur optique et servira de réfé-
rence à toutes les grandeurs caractéristiques angulaires
ou fréquentielles,
- la longueur d’un tour N
1
·
∆
θ
1
si le codeur présente une
résolution de N
1
point par tour,
- la longueur de la fenêtre de la TFD N·
∆
θ
1
si la Transformée
de Fourier est calculée sur N points.
Fig. 7 : Caractéristiques périodiques d’une géométrie
présentant z
1
éléments discrets
L’écriture des relations entre les différentes périodes et
leur localisation fréquentielle permet d’obtenir les expres-
sions suivantes :
- pour la fréquence d’échantillonnage
,
- la fréquence d’engrènement
,
- la résolution fréquentielle
.
Des relations précédentes, il suffit d’imposer une longueur
particulière à la fenêtre choisie pour effectuer la TFD
pour que la fréquence d’engrènement soit localisée
sur un multiple entier de la résolution fréquentielle.
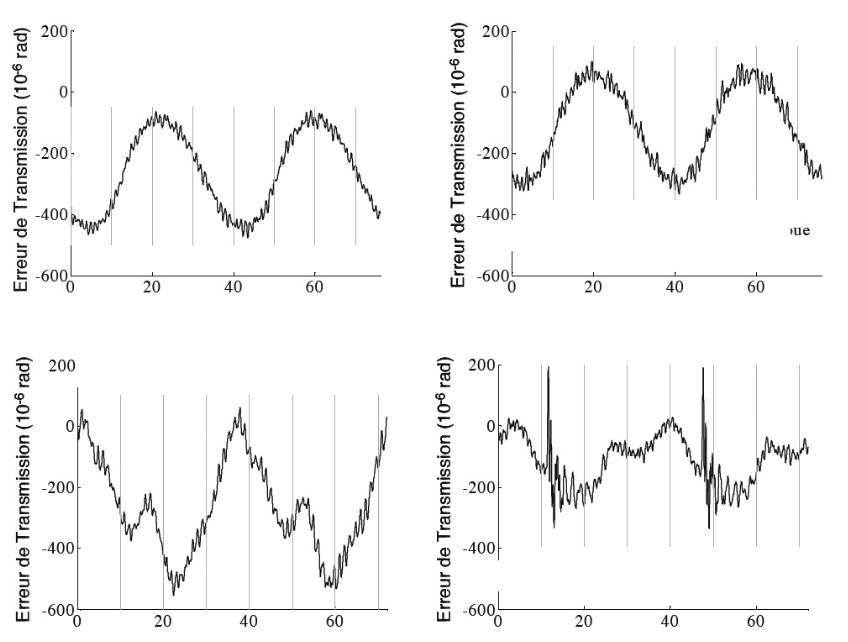
Fig. 5 : Mesure d’Erreur de Transmission d’un couple d’engrenages sains (a et c) et d’un couple d’engrenages présentant un défaut (b et d)
(a) sans défaut, échantillonage en référence à la roue
(b) avec défaut, échantillonage en référence à la roue
(c) sans défaut, échantillonage en référence au pignon
(d) avec défaut, échantillonage en référence au pignon

