Version HTML de base

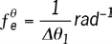
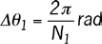
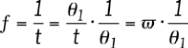
20
Mesure haute précision de vitesse angulaire instantanée pour la surveillance et la caractérisation d’excitation en machine tournante
En d’autres termes, il suffit que la longueur de la fenêtre
de la Transformée de Fourier Discrète N soit un multiple
de la résolution du codeur N
1
pour que l’on obtienne :
(4)
Cette condition ne fait pas intervenir le nombre de dents z
1
et reste valable quelle que soit la vitesse de rotation.
Parce qu’elle reste vraie pour tous les harmoniques de
la fréquence d’engrènement, elle permet donc d’assurer
que l’estimation du niveau de ces harmoniques est opti-
male quelle que soit la vitesse de rotation.
Par ailleurs, on montre qu’il n’est pas nécessaire d’ap-
parier la résolution du codeur à la géométrie discrète.
Comparativement, l’échantillonnage temporel associé à une
TFD introduit une erreur systématique liée aux fluctuations
de vitesse et à la méthode d’acquisition des signaux.
Application à l’estimation correcte du niveau des
harmoniques de l’excitation
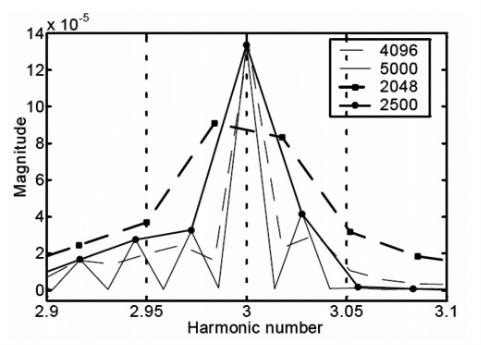
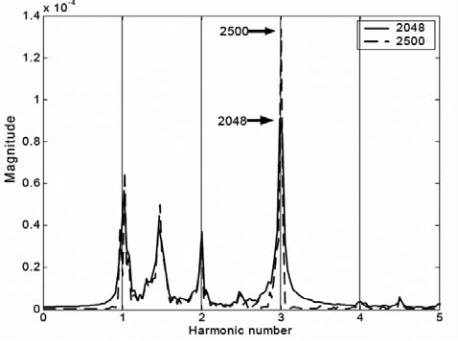
Afin d’illustrer cette propriété, des mesures d’Erreur de
Transmission sur des engrenages présentant un rapport
de réduction de 36/38 sont réalisées à l’aide de codeurs
optiques ayant chacun une résolution de 2 500 traits par
tour (N
1
=N
2
=2 500). La figure 8(a) montre la différence
du niveau estimé par exemple sur le troisième harmoni-
que de la TFD de l’Erreur de Transmission à 0,9.10
-4
rad
si la longueur de la fenêtre est de 2 048 points, alors que
le niveau réel est de 1,35.10
-4
rad est estimé en choisis-
sant la longueur de la fenêtre égale à la résolution du
codeur optique.
La figure 8(b) illustre clairement qu’il est nécessaire
d’avoir une longueur de la fenêtre d’analyse de la TFD qui
soit un multiple de la résolution du codeur pour obtenir
une estimation correcte. Elle met également en évidence
qu’il n’est pas nécessaire d’avoir une longueur d’analyse
supérieure à la résolution du codeur pour obtenir une
estimation correcte du niveau des raies latérales liées
à une modulation à la fréquence de rotation de l’arbre.
D’autres résultats complémentaires sur ce point ont été
développés dans [13].
Application à l’estimation fréquentielle à vitesse variable
Théoriquement, la comparaison dans le domaine fréquen-
tiel de signaux échantillonnés temporellement pour deux
conditions de vitesse différentes sur une machine tournante
n’est pas valable puisque le changement de vitesse intro-
duit un artefact lié aux conditions d’échantillonnage.
L’échantillonnage angulaire s’avère donc particulièrement
intéressant pour des mesures à vitesse variable, les condi-
tions d’échantillonnage ne variant pas dans ce cas. En effet,
les signaux sont alors exprimés en fonction de la position
angulaire du codeur de référence qui joue le même rôle que
le temps dans une transformée de Fourier classique. La
fréquence angulaire ƒ
θ
est une variable homogène à 1/
θ
1
dont on rappelle que la plus grande valeur accessible est
où
est la résolution
angulaire du codeur de référence ayant N
1
traits par tour.
Dans ce contexte, une représentation de type diagramme de
Campbell (évolution des fréquences propres en fonction de la
vitesse de rotation), présentant l’évolution de toutes les compo-
santes fréquentielles en fonction de la vitesse de rotation, va
être inversée dans le cas d’un échantillonnage angulaire.
Dans le cas d’un échantillonnage temporel, la figure 9(a) montre
que les fréquences de résonance de structure sont locali-
sées à une fréquence fixe lorsque la vitesse augmente. Les
composantes fréquentielles, multiples de la vitesse de rota-
tion (on parle d’ordres), voient leur localisation fréquentielle
augmenter linéairement avec cette vitesse de rotation.
Dans le cas de l’échantillonnage angulaire présenté sur
la figure 9(b) les fréquences de résonance de structure
apparaissent sous forme d’hyperboles parce qu’elles sont
localisées à une fréquence fixe :
(5)
Quant aux composantes multiples de la vitesse de rota-
tion, elles sont localisées à une fréquence qui évolue avec
la vitesse, elles apparaîtront alors sous forme de lignes
verticales parallèles à l’axe des vitesses.
Des mesures d’Erreur de Transmission ont été réalisées
sur le banc d’essais d’un train simple étage lors d’une
montée en vitesse de 0 à 6 000 tr/min en 20 secondes.
Fig. 8 : Différence de niveau enregistrée sur les harmoniques de l’Erreur de Transmission pour deux longueurs de fenêtre

