Version HTML de base


36
Caractérisation dynamique des matériaux et réduction des nuisances vibroacoustiques : l’apport des vibrations. Partie 1
Vibration forcée en dehors de la résonance
Cette technique de caractérisation concerne l’Analyse
Mécanique Dynamique (AMD) ou Dynamic Mechanical
Analysis (DMA) en anglais, elle met en œuvre la vibration
forcée en dehors de la résonance.
Un déplacement d’amplitude Ao est appliqué à l’échan-
tillon et on mesure la force dynamique transmise Fo. Ce
qui revient à mesurer la raideur de l’échantillon en vertu de
la relation classique de la RDM entre contrainte et défor-
mation. Notons que cette grandeur (raideur) s’exprime en
N/m, elle dépend de la géométrie de l’échantillon et n’est
donc pas une caractéristique intrinsèque du matériau.
Comme nous l’avons déjà évoqué, la réponse des maté-
riaux viscoélastiques à une sollicitation harmonique n’est
pas instantanée, mais déphasée (voir figure 6). Les mesu-
res sont traitées par transformée de Fourier rapide pour
extraire le module et le déphasage entre signaux. Ensuite
le passage aux caractéristiques intrinsèques du matériau
(module de Young E, module de cisaillement G, module de
flexion Ef, viscosité h
h
…) est obtenu par application d’un
facteur de forme. A titre d’exemple la figure 15 présente un
Analyseur Mécanique dynamique (AMD) METRAVIB.
Fig. 15 : Bâti DMA+ 150N (vue détaillée de la colonne de mesure)
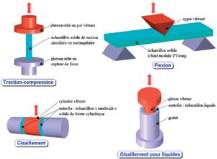
Fig. 16 : DMA - principaux modes de sollicitation
Les principaux modes de sollicitation sont illustrés figure
16. Pour chaque mode et une géométrie définie, un facteur
de forme permet de passer de la mesure de la raideur aux
caractéristiques intrinsèques du matériau.
Par exemple si nous choisissons le mode traction-com-
pression le facteur de forme de l’éprouvette F
f
(figure 17)
est égal à :
F
f
=h/S
e
en m
-1
Avec :
h : hauteur (m)
S
e
: surface excitée (m
2
)
En général les échantillons sont collés sur les interfaces
mécaniques, ce qui se traduit lors des phases de compres-
sion et de tension par des déformations non uniformes des
surfaces latérales (tonneau ou diabolo), figure 17.
Fig. 17 : Modes de déformation d’un échantillon
collé aux extrémités
Un facteur correctif Fc, permet de prendre en compte cet
effet qui est d’autant plus marqué que le ratio diamètre
sur hauteur est élevé.
€
F
c
=
1
1
+
2
S
e
S
l
2
avec : S
l
= surface latérale (m
2
)
Le mode de sollicitation traction-compression encastré
n’est pas pur et fait intervenir les composantes E et G.
Le préfixe 2 dans l’expression F
0
correspond au matériau
incompressible pour lequel E = 3G ou
ν
=0,5. Si cette
hypothèse est satisfaisante pour les élastomères elle
n’est qu’approchée pour d’autres matériaux, il faut alors
tenir compte du coefficient de Poisson.
Finalement les mesures de la raideur en partie réelle k’ et
partie imaginaire k’’ multipliées par les facteurs de forme
et de correction donnent les composantes du module
d’Young E*.
E’(
ω
,T)=k’F
ƒ
F
c
=k.F
ƒ
.F.cos(
δ
)
E"(
ω
,T)=k"F
ƒ
F
c
=k.F
ƒ
.F.sin(
δ
)
η
=E"/E’=tan(
δ)
Les principaux facteurs d’influence sur les propriétés dynami-
ques des polymères et des élastomères sont dans l’ordre :
la température, la fréquence et le taux de déformation.

