Version HTML de base

37
Caractérisation dynamique des matériaux et réduction des nuisances vibroacoustiques : l’apport des vibrations. Partie 1
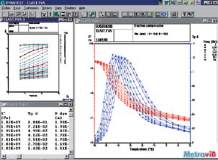
Fig. 18 : Spectre typique d’un élastomère
(-60°C<T<30°C ; 5Hz>f<200Hz). Partie droite :
isochrones ; partie gauche : isothermes
En partant des basses températures vers les hautes tempé-
ratures, le matériau viscoélastique passe (figure 18) :
- du domaine vitreux (les entités sont figées) où le module
varie peu et où l’amortissement est faible, à la zone de tran-
sition vitreuse Tg dans laquelle il y a réarrangement des
entités moléculaires.
Cette zone peut s’étendre sur plusieurs dizaines de degrés,
le module peut varier de plusieurs ordres de grandeur et
l’amortissement passe par un maximum caractéristique de
la capacité du matériau à dégrader de l’énergie sous forme
de chaleur; ou à un domaine caoutchoutique où les propriétés
mécaniques se stabilisent et l’amortissement décroît.
Pour certains matériaux (par exemple thermoplastiques),
le plateau est suivi d’une zone de fusion accompagné d’une
chute de module et d’une augmentation de l’amortissement
(on tend vers le fluide visqueux pour lequel la force est propor-
tionnelle à la vitesse ce qui correspond à une tangente de l’an-
gle de perte infinie).
L’influence de la fréquence est inverse. Plus elle croît et plus
le module augmente pour décrire le comportement inverse
à celui observé lorsque la température augmente.
Schématiquement nous pouvons dire que :
- lorsque la température augmente à fréquence impo-
sée, la mobilité des chaines croît et tend à faire chuter le
module (augmentation de l’entropie);
- lorsque la fréquence augmente à température fixe, le
matériau qui est défini par un temps caractéristique (en
fait une distribution de temps de relaxation) va répondre
différemment suivant que la fréquence de sollicitation est
inférieure ou supérieure à ce temps.
Nous venons de voir que l’augmentation de la tempéra-
ture d’une certaine valeur conduit aux mêmes change-
ments des propriétés qu’une diminution appropriée de la
fréquence et inversement. Pour le module d’un matériau
homogène, amorphe et isotrope, la relation s’écrit :
M(T
1
,ƒ
1
)=M(T
2
,ƒ
2
)
Cette relation traduit le principe de superposition temps-
température qui permet d’élargir artificiellement le domaine
de fréquence expérimental (limité pratiquement à quel-
ques décades), figure 19.
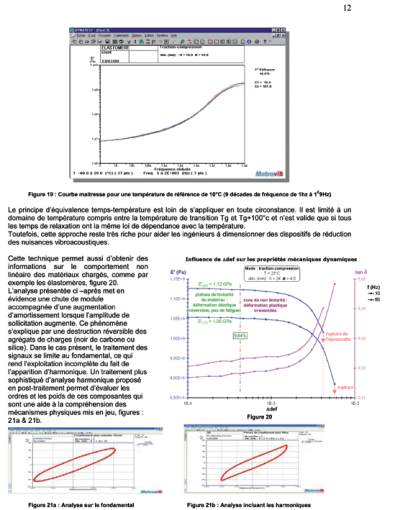
Fig. 19 : Courbe maîtresse pour une température de référence
de 10°C (9 décades de fréquence de 1Hz à 1
E
9Hz)
Le principe d’équivalence temps-température est loin
de s’appliquer en toute circonstance. Il est limité à un
domaine de température compris entre la température
de transition Tg et Tg+100°c et n’est valide que si tous
les temps de relaxation ont la même loi de dépendance
avec la température.
Toutefois, cette approche reste très riche pour aider
les ingénieurs à dimensionner des dispositifs de réduc-
tion des nuisances vibroacoustiques. Cette technique
permet aussi d’obtenir des informations sur le compor-
tement non linéaire des matériaux chargés, comme par
exemple les élastomères, figure 20.
Fig. 20 : Influence de
D
def sur les propriétés dynamiques
L’analyse présentée ci-après met en évidence une chute
de module accompagnée d’une augmentation d’amortis-
sement lorsque l’amplitude de sollicitation augmente. Ce
phénomène s’explique par une destruction réversible des
agrégats de charges (noir de carbone ou silice). Dans le
cas présent, le traitement des signaux se limite au fonda-
mental, ce qui rend l’exploitation incomplète du fait de
l’apparition d’harmonique.
Un traitement plus sophistiqué d’analyse harmonique
proposé en post-traitement permet d’évaluer les ordres
et les poids de ces composantes qui sont une aide à la
compréhension des mécanismes physiques mis en jeu,
figures : 21a & 21b, page suivante.

