Version HTML de base
26
L’analyse modale expérimentale
Considérons maintenant l’exemple d’une poutre fixée à
une extrémité, comme sur la figure 6.
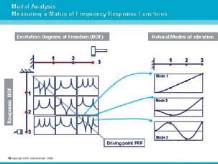
Fig. 6 : Exemple d’une poutre
Si la poutre est excitée au point 3 et que sa réponse
est mesurée au même point, la fonction de réponse en
fréquence obtenue pour la sortie 3 et l’entrée 3 (la sortie
est la réponse de la structure, tandis que l’entrée est la
force exercée) est présentée sur la figure 6. Dans ce cas,
la mesure se fait au même point pour l’entrée et la sortie.
C’est la mesure au point d’excitation (« driving point »).
Etudions maintenant la fonction de réponse en fréquence :
elle possède précisément trois pics, ce qui indique qu’il
y a trois fréquences de résonance. On peut refaire le
même test en frappant la poutre aux points 1 et 2 tout
en gardant l’accéléromètre au point 3. On obtient alors la
troisième ligne de la matrice de la fonction de réponse en
fréquence. Ce procédé s’appelle un essai de marteau de
choc. Bien évidemment, on peut également utiliser un pot
vibrant au point 3 et placer l’accéléromètre aux points 1,
2 ou 3 afin de mesurer les mêmes fonctions de réponse
en fréquence. Dans ce cas, les réponses des trois points
sont mesurées simultanément.
D’un point de vue théorique, il n’y a aucune différence entre
un essai effectué avec un marteau de choc et un essai
effectué avec un pot vibrant. Cependant, dans la réalité,
la liaison entre le pot vibrant et la structure peut apporter
une certaine raideur à l’ensemble. Une autre différence
entre les deux types d’essais peut également provenir de
la masse des accéléromètres. Si ces derniers sont repo-
sitionnés après chaque essai, la répartition des masses
peut changer. Par conséquent, il y aura un décalage de la
fréquence de résonance dans les fonctions de réponse
en fréquence. Une solution possible pour éviter de modi-
fier la répartition des masses serait de placer une masse
fictive sur la structure.
Si l’on prend la partie imaginaire obtenue à une fréquence
de résonance particulière dans chaque fonction de réponse
en fréquence, on peut alors représenter la déformation
de la poutre. Sur la figure 6, on peut observer les trois
premières fréquences de résonances et constater la défor-
mation de la poutre pour une fréquence particulière. En
étudiant plus attentivement les fonctions de réponse en
fréquence, on peut noter que, lorsque l’on frappe la poutre
au point 2, on ne génère que deux pics. On peut expliquer
ce phénomène en posant que le point 2 est un point avec
zéro déformation pour la deuxième fréquence de réso-
nance. On appelle ce point un nœud. Il s’agit de l’un des
aspects les plus importants de l’analyse modale expéri-
mentale. Un nœud ne peut jamais être un point d’excita-
tion : si l’on ne frappe la poutre qu’au point 2, on ne sera
donc pas en mesure d’identifier la deuxième fréquence
de résonance.
On savait déjà que la caractéristique modale d’une struc-
ture était définie par la fréquence de résonance, le facteur
d’amortissement et les déformées modales. L’étude de la
poutre nous montre que l’on peut identifier la fréquence
de résonance et la déformation à partir des fonctions de
réponse en fréquence.
Aujourd’hui, de nombreux estimateurs de paramètres modaux
sont disponibles pour la résolution des cas à multiples
degrés de liberté. Une difficulté est l’identification des modes
amortis, en particulier en haute fréquence. On notera que
la connaissance de l’amortissement est une question déli-
cate, qu’il soit interne, ou externe (notamment en raison du
rayonnement acoustique) ; dans la plupart des situations,
il rend les déformées modales complexes, c’est-à-dire que
la déformée modale change dans le temps.
Déformées ou déformées opérationnelles
Lorsque l’on a évoqué les caractéristiques dynamiques
d’une structure, on a parlé de déformées. Quelle est la
différence entre une déformée (modale) et une déformée
opérationnelle ? Les modes sont des ensembles uniques
de solutions qui décrivent les caractéristiques modales
d’une structure. Seules, une modification de la masse,
de l’amortissement et de la raideur peuvent modifier les
caractéristiques modales d’une structure. Ainsi, une défor-
mée ne peut être modifiée que par une modification de
la masse, de l’amortissement ou de la raideur.
La déformée opérationnelle est la réponse d’une structure
à une force appliquée en conditions opératoires. La défor-
mée opérationnelle varie en fonction de la force appliquée
et des conditions opératoires.
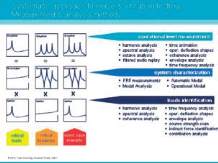
Fig. 7 : Approche systématique des essais de bruit et vibrations
Sur la figure 7, on voit que la déformée opérationnelle
mesure la réponse de la structure au niveau du récepteur.

