Version HTML de base


27
L’analyse modale expérimentale
La caractéristique modale est définie, elle, au niveau du
transmetteur. Lorsque l’on applique différente charges, la
déformée opérationnelle résultante est ajustée et change.
Bien qu’elle constitue une méthode rapide et très visuelle
pour estimer la déformation de la structure, l’observa-
tion de la déformée opérationnelle ne fournit que des
informations sur la façon dont la structure bouge et
sur les parties de cette structure qui se tordent ou
se plient le plus sous l’effet de certaines charges de
fonctionnement.
La déformée opérationnelle est une combinaison linéaire
de déformées modales. Autrement dit, chaque structure
possède ses propres caractéristiques dynamiques, qui
constituent un modèle modal. Ce modèle exprime simple-
ment la dynamique de la structure dans l’espace modal,
plutôt que dans le domaine temporel ou fréquentiel. Le
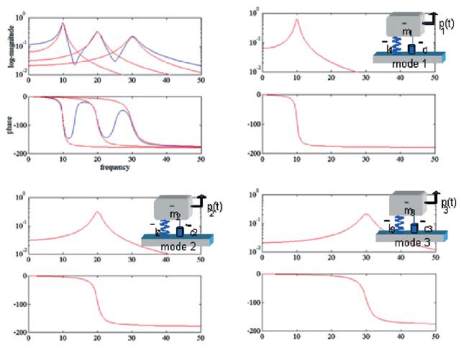
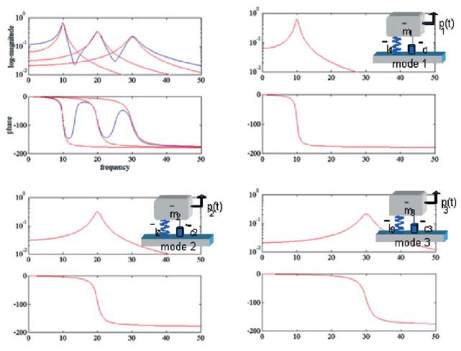
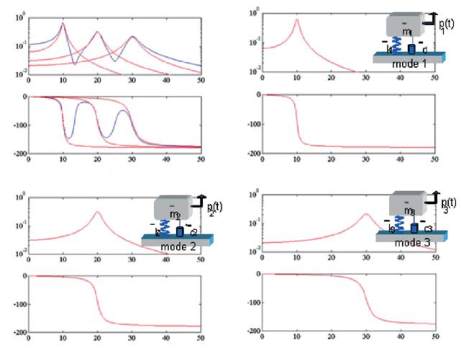
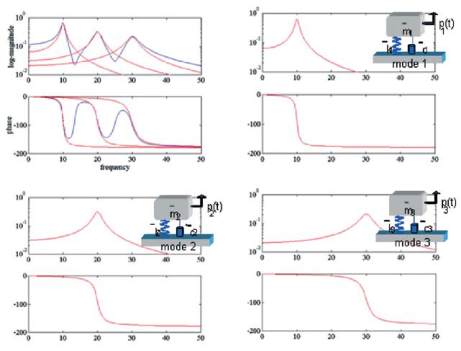
modèle modal, par exemple un modèle à trois degrés de
liberté comme celui présenté dans la figure 8, consiste
en un ensemble de modes : mode 1, mode 2 et mode 3.
On obtient une fonction de réponse en fréquence par la
somme (figure 8, courbe bleue sur le graphe supérieur)
des modes individuels (figure 8, courbe rouge).
Analyse modale analytique
Dans l’analyse modale expérimentale, nous avons utilisé
un modèle physique avec un nombre limité de points
mesurés. Les données temporelles mesurées ont été
converties en données fréquentielles. La matrice de la
fonction de réponse en fréquence a été résolue à l’aide
d’une méthode d’estimation des paramètres modaux et
l’on a obtenu un ensemble unique de modes que l’on a
appelé le modèle modal.
L’analyse modale analytique constitue une autre méthode
d’analyse modale qui commence par l’estimation de la
répartition des masses, des raideurs et de l’amortisse-
ment dans la structure au moyen des matrices masse,
raideur, amortissement ([M], [K], [C]).
Ces dernières définissent l’équation propre :
où p est la variable du domaine de Laplace et
Les valeurs propres contiennent le facteur d’amortisse-
ment et la fréquence naturelle, les vecteurs propres sont
liés aux déformées modales. Le modèle analytique est
combiné avec la solution propre du modèle aux éléments
finis présentés dans la figure 9.
Figure 8. Exemple d’un modèle à 3 degrés de liberté
Phase
Log-Magnitude
Frequency

