Version HTML de base
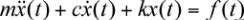




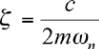
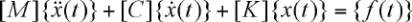
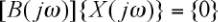
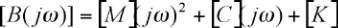
25
L’analyse modale expérimentale
L’équilibre des forces d’un système à un degré de liberté
s’exprime à l’aide des forces d’inertie, de l’amortissement,
de la raideur et de forces externes :
où m est la masse, c l’amortissement, k la raideur,
sont, respectivement, l’accélération, la vélocité et le
déplacement, ƒ est la force externe et t est la variable
temps. Après transformation dans le domaine fréquen-
tiel, l’équation du domaine temporel s’exprime sous la
forme
où
ω
est la variable fréquence. On définit la fonction
de transfert comme le rapport de la réponse d’une
structure sur la force exercée. La solution de l’équation
est la fréquence propre
2
de
l’exemple à un degré de liberté. La fréquence de réso-
nance s’exprime alors sous la forme
et le facteur d’amortissement est
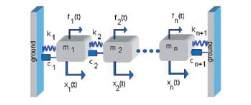
On peut étendre le concept du degré de liberté unique
à un système à plusieurs degrés de liberté, comme le
montre la figure 4.
Fig. 4 : Système à plusieurs degrés de liberté
Dans ce cas, on utilise une équation matricielle pour
décrire le système.
est l’équation dans le domaine temporel et l’espace physi-
que, avec une matrice de masse, une matrice d’amortis-
sement et une matrice de raideur.
Il est plus facile de résoudre les équations en les trans-
posant dans le domaine fréquentiel. La solution non triviale
de l’équation
est un ensem-
ble unique de valeurs propres et de vecteurs propres
complexes, où
La partie réelle de la valeur propre est l’amortissement,
tandis que la partie imaginaire est la fréquence de réso-
nance. Le vecteur propre représente, quant à lui, la défor-
mée modale.
Fonctions de réponse en fréquence
Les fonctions de transfert sont également appelées fonc-
tions de réponses en fréquence (FRF). Pour mesurer la
fonction de transfert, on suspend par exemple la struc-
ture, avec comme conditions aux limites, les deux extrémi-
tés libres ou une extrémité fixée. Plusieurs capteurs, tels
que des accéléromètres, sont placés sur la structure. On
applique une force sur la structure à l’aide d’un marteau
de choc ou d’un pot vibrant. La force et la réponse de la
structure sont mesurées simultanément par un système
d’acquisition ou par un analyseur. Les fonctions de répon-
ses en fréquence sont traitées par ordinateur relié au
système d’acquisition. Les données temporelles mesu-
rées sont converties du domaine temporel au domaine
fréquentiel au moyen d’un algorithme de transformée de
Fourier rapide (FFT) et la fonction de réponse en fréquence
est traitée par un logiciel. Les fonctions de réponse en
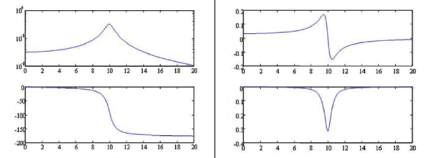
fréquence sont présentées dans la figure 5 sous diffé-
rents formats. A la fréquence de résonance, la fonction
de réponse en fréquence présente un pic d’amplitude et
la phase chute de 180°. La partie réelle de la fonction de
réponse en fréquence est égale à zéro et la partie imagi-
naire atteint un pic.
Fig. 5 : Fonction de réponse en fréquence amplitude/force autour d’une résonance :
à gauche, amplitude (haut) et argument (bas) ; à droite, parties réelle (haut) et imaginaire (bas).
2- C’est une quantité complexe, dont la partie réelle correspond à une fréquence,
et la partie imaginaire à une décroissance de la vibration. La fréquence de résonance
est très proche de la partie réelle. On dit indifféremment « propre » ou « naturelle ».
Frequency Response Function
Frequency Response Function
Frequency Hz
Real Part
Imaginary Part
Phase
Log-Magnitude
Frequency Hz
Frequency Hz
Frequency Hz

