Version HTML de base
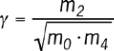

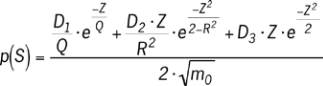
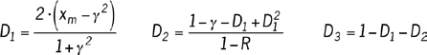
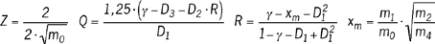
20
Accélération des essais en environnement mécanique. Apports de la simulation numérique à l’approche physique
Le terme entre crochets dans l’équation (3) est la distri-
bution des probabilités de Rayleigh.
La solution «bandes fines» de Bendat a tendance à être
conservatrice pour les signaux larges bandes.
Rice [4] a proposé une mesure fiable de la bande passante
sous la forme du rapport du nombre de dépassements de zéro
avec pente positive dans un signal temporel sur le nombre
de pics. Ce rapport, souvent appelé «facteur d’irrégularité»,
est donné par l’équation (5). Pour les signaux «bandes fines»,
le facteur d’irrégularité tend vers 1, tandis que les signaux
«larges bandes» tendent progressivement vers zéro.
Dirlik
Rice a conclu que pour un signal de bande passante quel-
conque, on pouvait obtenir la fdp des pics à partir de la
somme pondérée des distributions de Rayleigh et de Gauss.
Cependant, la fdp des pics n’est pas identique à la fdp de
la gamme de contraintes dont on a besoin pour l’analyse
de la fatigue. En 1985, Dirlik [5] a proposé une solution
analytique empirique pour estimer la fdp de l’étendue des
contraintes basée sur de longues simulations numériques
utilisant la technique de Monte Carlo. Apparemment bien
plus compliquée que certaines autres méthodes, il ne
s’agit que d’une fonction de quatre moments de la surface
de la DSP, m
0
, m
1
, m
2
et m
4
. La formulation de Dirlik est
donnée par les équations 7 et 8.
où, N(S) est le nombre de cycles de contraintes d’éten-
due S N/mm
2
attendu pour la période T sec. E[P] est le
nombre de pics attendu, obtenu par l’équation (4).
(5)
(7)
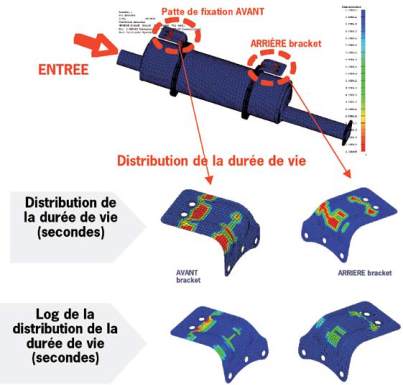
Fig. 9 : Cartographie de l’endommagement sur le pot d’échappement et ses fixations
(8)

