Version HTML de base

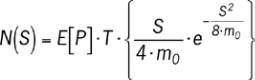
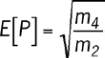
19
Accélération des essais en environnement mécanique. Apports de la simulation numérique à l’approche physique
La figure 7 représente le modèle «éléments finis» et ses
conditions aux limites. La DSP appliquée par chargement
au point d’excitation est l’enveloppe des DSP avant et
arrière. Des éléments rigides relient le point d’excitation
aux pattes de fixation (à l’endroit où elles sont montés
sur les organes du châssis).
Fig. 7 : Modèle «éléments finis» obtenu par
l’essai vibratoire virtuel
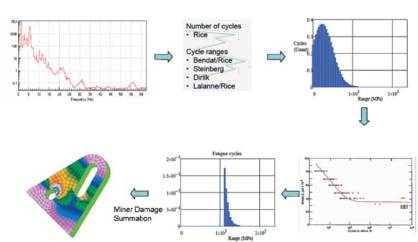
On évalue l’endommagement pour chaque nœud du compo-
sant à l’aide de la procédure illustrée sur la figure 8.
Le compteur de cycles DSP est crucial dans cette procé-
dure. Les compteurs les plus courants sont décrits et
comparés dans le paragraphe suivant.
Compteurs de cycles DSP
Cette partie décrit les trois approches possibles utili -
sées pour le calcul de la résistance à la fatigue, ou de
l’endommagement, directement à partir des DSP des
contraintes et non à partir du signal temporel. Pour plus
d’informations sur le sujet, voir Bishop et Sherratt [1] et
Halfpenny [2], [7].
Méthode bandes fines (Bendat et Rice)
En 1964, Bendat [3] a proposé le premier pas signifi-
catif vers une méthode de détermination de la durée
de vie à partir des DSP. Dix ans plus tôt, en 1954, Rice
[4] avait montré que la fonction de densité de probabi -
lité (fdp) des pics pour un signal en bandes fines tendait
vers une distribution de Rayleigh lorsque la bande
passante diminuait. Si l’on utilise cette hypothèse, la
fdp de la gamme des contraintes tendrait également
vers une distribution de Rayleigh. Afin de finaliser sa
solution, Bendat a utilisé une série d’équations dérivées
par Rice [4] pour estimer le nombre de cycles attendus
en utilisant les moments de la surface sous les DSP. La
solution «bandes fine» de Bendat pour l’histogramme
des contraintes est donc déterminée à partir de la fdp
exprimée dans l’équation (3).
où N est le nombre de cycles attendus pour la gamme de
contraintes S se déroulant pendant T secondes. m
0
est le
zéroième moment de la surface de la DSP, et E[P] est le
nombre de pics attendu obtenu par l’équation (4).
m
4
et m
2
sont respectivement les 4
e
et 2
e
moments de
la surface de la DSP où le n
ième
moment de la surface est
défini par
€
m
n
=
f
∫
n
⋅
G f
( )
df
, et G(ƒ) est la valeur de la DSP
à une seule bande à la fréquence de ƒHz.
Fig. 8 : Déroulement de l’analyse de la fatigue vibratoire
(3)
(4)
PSD of Stress at each node
PSD Cycle Counting
Rainflow Histogram
LIFE
Damage Histogram Material SN Curve

