Version HTML de base
Spécial “ 5es Assises sonore ”
67
Acoustique
&
Techniques n° 51
La prévision du bruit de trafic en milieu urbain : apport de la modélisation dynamique
Sachant que la relation (3) est en permanence vérifiée, le
modèle LWR se réduit à une seule équation de la variable
K (4) :
K
t
+
Q
eq
(K)
x
=
0
(4)
Les premiers développements du modèle Symubruit
utilisaient une résolution macroscopique de ce modèle,
en estimant la densité de véhicules présents à chaque
incrémentation temporelle dans les cellules du réseau.
Des avancées récentes [5], [6], [7] ont permis de
développer une méthode de résolution plus performante
et mieux adaptée à un couplage avec des lois d’émission
acoustique.
Il s’agit d’une résolution lagrangienne représentant les
positions des véhicules sur le réseau à chaque instant
de simulation tout en gardant une loi de comportement
macroscopique garante de la bonne représentation de la
physique de l’écoulement. La résolution de l’équation (1)
conduit à l’expression de la position du ième véhicule à
l’instant t :
(5)
avec :
t
=
1 wK
max
(
)
représentant le pas de discrétisation
temporel
- v
max
: vitesse maximale possible lorsque le trafic est
fluide
-
ν
i
t
: vitesse du véhicule i à l’instant t
- s
min
= 1/Kmax : inverse de la concentration maximale
(cas d’une file arrêtée)
- A : accélération maximale.
Ce modèle a été complété par un certain nombre
d’extensions permettant :
- La modélisation des restrictions de
capacité mobile [8] pour représenter
les véhicules ayant des comportements
cinématiques spécifiques (par ex.
transports en commun) par rapport au
reste de la circulation ;
- La modélisation différenciée des voies
de circulation avec la gestion associée
des changements de voie [9], [10] ;
- La représentation simplifiée des
carrefours par affectation des véhicules
en sortie des tronçons amont en
entrée des tronçons aval au moyen de
coefficients directionnels.
Des recherches sont en cours pour
intégrer la description des carrefours
complexes en intégrant la description
des conflits entre flux antagonistes.
L’émission des classes de véhicules et la
représentation des sources de bruit
Le calcul des émissions acoustiques par cellule s’effectue
comme suit :
- Le modèle de trafic détermine, pour la cellule n°j et
l’instant t, les paramètres suivants :
- Le nombre de véhicules légers et de véhicules de
transports en commun présents dans la cellule. Les
véhicules légers sont supposés être identiques du point
de vue acoustique (véhicule « moyen »), ce qui est rendu
nécessaire par la représentation macroscopique du trafic.
L’émission du véhicule « moyen » résulte d’une synthèse
des émissions mesurées sur un panel représentatif du
parc automobile actuel [11] :
- Leurs paramètres cinématiques : vitesse, allure (accélérée
/ décélérée / stabilisée).
- La connaissance de ces paramètres associés aux lois
d’émission correspondantes permet de calculer la puissance
acoustique totale émise par la cellule à l’instant t :
L
w
T . j
(t )
=
n
x
(t )L
w
VL. j
L
W
TC i
, j
(t )
i
(6)
(sommation au sens énergétique des puissances
acoustiques émises par les VL – la concentration K prend
en compte le nombre de véhicules présents dans la cellule
à l‘instant t – et des autobus)
La cellule est assimilée à une ligne source. A un point
d’observation donné, la cellule n°j est alors « vue » sous
l’angle d’exposition aj (fig. 3) Le L
Aeq1s
s’écrit, pour
l’ensemble des cellules :
LAeq
1s
(t )
=
10 log
j
L
W
T ,j
j
(7)
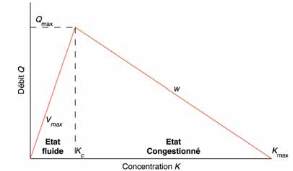
Fig. 2 : Diagramme fondamental illustrant la dépendance
existant entre débit de trafic et concentration

