Version HTML de base

Spécial “ 5es Assises sonore ”
51
Acoustique
&
Techniques n° 51
Prise en compte des effets météorologiques dans un modèle de propagation analytique pour la cartographie du bruit dans l’environnement
c(z)
=
c
0
1
+
z
R
On prouve théoriquement que les rayons sonores sont
alors des cercles ayant leur centre sur la ligne z = -R
[2,4]. Le projet Nord 2000 avait démontré comment les
formulations valables pour une atmosphère uniforme
pouvaient être adaptées au cas d’un gradient linéaire.
Toutefois, la construction géométrique de tels rayons se
heurte rapidement à des problèmes pratiques lorsque le site
comporte un ou plusieurs obstacles diffractants. D’autre
part, pour des gradients et/ou des distances de propagation
suffisamment grands, l’unique rayon réfléchi par le sol se
transforme en trois, cinq, sept,… rayons réfléchis, ce
qui complique encore les constructions géométriques et
introduit des discontinuités des résultats acoustiques au
passage des certaines valeurs limites.
Plusieurs auteurs [7,8] ont mis en évidence la similitude
entre la propagation du son au-dessus d’un sol plan en
présence d’un gradient de vitesse et la propagation sur
un sol courbe en absence de tels gradients (figure 3).
Mathématiquement, cette analogie résulte de l’application
d’une transformation conforme au problème initial. Après
transformation on se retrouve alors avec un nouveau
problème géométrique dans lequel on peut simuler une
propagation en milieu homogène et les méthodes décrites
ci-dessus s’appliquent. Appliquer la transformation inverse
permet de reconstruire rapidement les rayons sonores
dans le problème initial (figure 4 page suivante).
La méthode prédit l’existence d’un ou trois réflexions
géométriques en fonction de la distance et du gradient de
célérité. Toutefois, étant donné que chaque contribution
est pondérée par la zone de Fresnel correspondante,
les atténuations calculées sont continues au passage
de la limite.
Caractérisation des effets météorologiques
Le cas d’un gradient linéaire peut donc être traité avec rigueur
par des méthodes analytiques ; toutefois, ce cas théorique ne
correspond guère à la réalité. L’étape suivante, nécessaire au
développement d’une méthode opérationnelle, a donc été de
relier le modèle à une description plus proche de la situation
réelle. Cette opération a été menée par approximations
successives :
- D’abord, il a été admis que pour la propagation proche du
sol, les effets météorologiques puissent être modélisée par
une équation d’ondes classique en considérant une célérité
effective combinant les effets de température et de vitesse
du vent (voir encart page 58).
- Ensuite, il a été vérifié que les profils de célérité puissent
être approximées par des fonctions standards de type lin/
log : c
eff
(z)=c
o
+A.z+B.logz . Dans cette approche, les
effets météorologiques sur la propagation sont entièrement
déterminés par les valeurs des coefficients A et B.
- Enfin, une méthode originale a été développée permettant de
transformer les profils lin/log en un gradient linéaire équivalent
en fonction de la distance de propagation et de la hauteur de
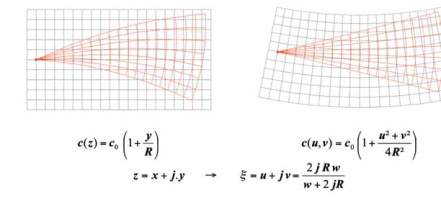
Fig. 3 : Le gradient de célérité définit sur le domaine d’origine une métrique de Poincaré. Les rayons sonores sont
les géodésiques de cette espace ; en particulier, ce sont des cercles ayant leur centre sur la ligne y= -R.
La transformation de Möbius fait correspondre à chaque position (x,y) du domaine initial, une position (u,v)
dans le domaine transformé. Dans le domaine ainsi transformé, les géodésiques passant par l’origine sont
des droites. La célérité du son a également été modifiée en une fonction radiale. Pour des valeurs :
d = u? + v?
<<
R
on peut négliger cette dépendance et poser :
c u, v
( )
c
0
The sound speed gradient defines a Poincaré metric in the original space. Ray paths coincide with the geodesic
lines in this space ; i.e. they correspond to circles with center on the line y= -R. The Möbius transform maps
the original space (x,y) into a new space (u,v). In this transformed space geodesics through the origin are
straight lines. The sound speed transforms into a radial function. For sufficiently short distances
d = u? + v?
<<
R
this can be approximately as:
c u, v
( )
c
0

