Version HTML de base

52
Spécial “ 5es Assises sonore ”
Acoustique
&
Techniques n° 51
Prise en compte des effets météorologiques dans un modèle de propagation analytique pour la cartographie du bruit dans l’environnement
la source. Dans cette approche, les effets météorologiques
sont entièrement déterminés par l’unique paramètre R, ou, ce
qui s’avère plus pratique, du paramètre sans dimensions R/D,
où D est la distance de propagation.
Lien avec la modélisation météorologique
La méthode décrite permet de relier directement les
paramètres A, B et R aux profiles de température T(z) et de
vitesse du vent u(z). La dernière étape du développement a
consisté à fournir une méthode simple permettant le calcul de
ces profils en fonction de paramètres directement accessible
à la mesure et à la prévision.
La méthodologie retenue est basée sur une approche similaire
à celle pratiquée pour la prévision de la dispersion des
polluants atmosphériques[2,9]. La théorie de similitude fournit
une description paramétrique des profils sous la forme :
u z
( )
=
u
k
ln z
z
0
+
1
z
L
T z
( )
=
T
0
gz
c
P
+
T
k
ln z
z
0
+
2
z
L
où
Ψ
1
et
Ψ
2
sont des fonctions universelles déterminées
expérimentalement, k = 0,4, g = 9,81 m/s² et cp = 1005 J
kg
-1
K
-1
sont des constantes. Les autres paramètres peuvent
être estimées à partir de mesures spécifiques au cas par
cas, par exemple à partir de plusieurs capteurs montés sur
des mâts météorologiques ou en utilisant des anémomètres
triaxial.
Le paramètre L, nommé longueur de Monin-Obukhov, est une
mesure directe de la stabilité atmosphérique résultant des
forces thermiques en jeu. Il joue un rôle essentiel dans les
prévisions acoustiques puisqu’il introduit un fort couplage entre
les gradients de température et de vent (figure 5).
En considérant des approximations linéaires adéquates, il est
possible de relier les paramètres A et B du modèle acoustique
aux paramètres :
u ,T
,
1 L
(
)
du modèle météorologique.
En absence de données expérimentales ou simulées, il est
possible de donner une première estimation de ces paramètres
à partir de données macro-météorologiques (tableau 1).
Dans ce cas, les données d’entrée de la méthode se réduisent
aux seuls valeurs de :
- la vitesse du vent à 10 m du sol
- la direction du vent à 10 m du sol
- la classe de stabilité, déterminée par la condition jour/nuit
et la couverture nuageuse.
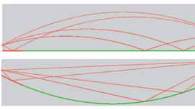
Fig. 4 : Le modèle d’ingénierie prend en compte la réfraction
météorologique en exploitant une analogie entre les rayons
sonores courbes ou dessus d’un sol plan et des rayons
droits réfléchis sur un sol courbe. Les deux modèles
prédisent l’existence de trois régions au sol, en accord
avec la méthode décrite dans la norme ISO 9613-2.
The engineering model takes into account meteorological
refraction based on an analogy between the propagation
of curved ray paths above a flat ground and straight ray
paths above a curved ground surface. Both models predict
the existence of three ground regions in accordance to
the method described in the ISO 9613-2 standard.
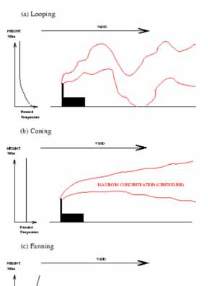
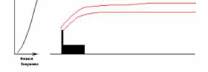
Fig. 5 : Stabilité de l’atmosphère et gradient de température
: atmosphère instable due à un fort ensoleillement (a)
; atmosphère neutre sans gradient de température en
cas de ciel couvert (b) et atmosphère stable au dessus
d’un sol froid, en cas de ciel de nuit dégagé (c). Les
gradients de température ont une influence directe sur
la vitesse de propagation du son et indirectement en
modifiant les profiles de vitesse du vent par brassage des
différentes couches d’air. la longueur de Monin-Obukov
est une mesure directe de cette interdépendance.
Atmospheric stability and thermal gradients: instable
atmosphere causes by heating of the ground by strong
sunshine (a), neutral atmosphere in case of heavy
cloud cover (b) and stable atmosphere due to cooling
of the ground under a clear night sky (c). Temperature
gradients have a direct influence on the sound speed
but also modify the wind speed profiles by mixing of
the different air layers. The Monin-Obukhov length
provides a direct measure of the interdependency
of temperature and wind speed profiles.

