Version HTML de base
50
Spécial “ 5es Assises sonore ”
Acoustique
&
Techniques n° 51
Prise en compte des effets météorologiques dans un modèle de propagation analytique pour la cartographie du bruit dans l’environnement
Dans la plupart des méthodes nationales en vigueur,
la modélisation de ces phénomènes est basée sur les
formulations empiriques contenues dans la norme ISO 9613-2,
veille de plus de 30 ans. Entre temps, de nombreux auteurs ont
proposés des modèles analytiques permettant de résoudre,
du moins partiellement, le problème posé : réflexion sur un
sol plan ou diffraction par un écran simple, avec ou sans
réfraction atmosphérique [1,2]. Le projet Nord 2000 [3,4]
peut être considéré comme une première tentative d’intégrer
ces éléments dans un modèle cohérent et complet et les
projets Harmonoise et Imagine se sont largement inspirés de
ces travaux en apportant toutefois une attention particulière
à la continuité des résultats, aux performances en temps
de calcul et à la détermination des paramètres d’entrée par
l’utilisateur final.
Dans un premier temps, le module de propagation a été
développé pour le cas d’un milieu uniforme et stationnaire et
c’est ce modèle que nous décrirons en premier, l’adaptation
du modèle aux effets météorologiques sera donnée dans le
paragraphe suivant.
L’entrée du module est constituée d’une séquence de
segments représentant la coupe en long correspondant au
chemin de propagation (figure 1).
Chaque segment est caractérisé par ses coordonnées (d, z)
et son impédance acoustique. Le principe du calcul consiste
alors à construire l’enveloppe convexe (c’est-à-dire le chemin
le plus court) passant au dessus de tout obstacle diffractant.
Conceptuellement, l’atténuation excédentaire s’écrit alors :
L
=
20 log p
p
free
=
L
D,k( i )
i
=
l
M
+
L
G,i
i
=
0
M
Où p
free
représente le niveau sonore en champ libre, c’est-à-dire
en absence de tout obstacle. Les termes
Δ
L
D,k(i)
représentent
la perte par insertion due à la diffraction et la somme porte
sur l’ensemble des points de l’enveloppe convexe ; ainsi
le modèle permet de calculer les cas de diffraction simple
par des écrans minces ou de diffraction multiple en cas de
plusieurs écrans ou d’obstacles épais. Les termes
Δ
L
G,i
correspondent à des réflexions sur le sol ou sur les faces
des obstacles diffractant ; le modèle n’imposant aucun
traitement particulier pour les uns ou les autres.
Les termes
Δ
L
D
sont évaluésselon laméthodesimplifiéeproposée
par [1], modifiée pour le cas des zones d’ombres profondes. Les
termes
Δ
L
G
sont calculés à partir des formulations analytiques
pour les coefficients de réflexion sphériques proposées par
Chien et Soroka [5]. Pour des formes complexes et/ou pour
des surfaces non-homogènes, les réflexions dues aux différents
segments sont pondérés en fonction de leur zone de Fresnel
[6], comme illustré à la figure 2.
L’implémentation de la méthode fait appel à une décomposition
récursive d’un problème complexe en autant de problèmes
élémentaires, ce qui limite les temps de calcul quelle que
soit la complexité géométrique du problème. L’utilisation
systématique de transitions permet de garantir une continuité
des résultats quels que soient les modèles élémentaires mis
en œuvre.
Prise en compte des effets météorologiques
Afin d’introduire les effets météorologiques dans un modèle
analytique de propagation, l’on considère en première
approximation le cas particulier d’un gradient linéaire de la
vitesse du son avec l’altitude au-dessus du sol :
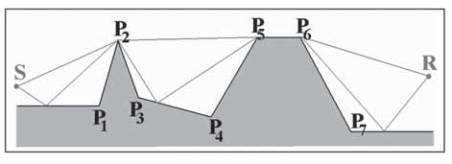
Fig. 1 : Profile en long en entrée du modèle et construction
de l’enveloppe convexe représentant le chemin de
propagation principal. Le calcul de l’atténuation
prend en compte les diffractions aux points P
2
(écran
mince), P
5
et P
6
(écran épais) et les effets de réflexions
sur les séquences de segments (S, P
1
, P
2
), (P
2
, P
3
,
P
4
, P
5
), (P
5
, P
6
) et (P
6
, P
7
, R) respectivement. Le
modèle traite de manière uniforme les réflexions sur
le sol et sur les faces des obstacles diffractant.
Cross section in the propagation plane and construction
of the convex hull representing the principal ray path.
The excess attenuation accounts for diffracting effects
at points P
2
(thin barrier), P
5
and P
6
(wide barrier) and
for reflections on the sequences of segments (S, P
1
,
P
2
), (P
2
, P
3
, P
4
, P
5
), (P
5
, P
6
) et (P
6
, P
7
, R). The model
uniformly treats reflections form ground segments
and from the faces of the diffracting obstacles.
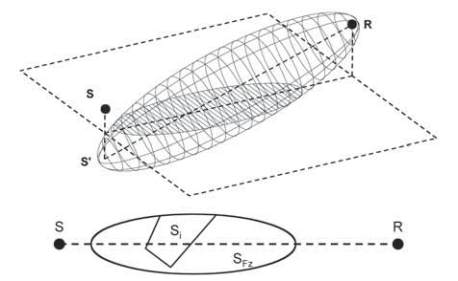
Fig. 2 : Pour un élément réfléchissant de dimensions finies
on construit l’ellipse de Fresnel en considérant les
positions du récepteur et de la source image par
rapport au plan infini porteur de cet élément. L’ellipse
de Fresnel correspond à la région du plan où :
dist S, X
(
)
+
dist X ,R
(
)
<
dist S,R
(
)
+
n .
La réflexion par l’obstacle est alors pondérée par un
facteur w
i
=S
i
/S
FZ
équivalent à la fraction de l’ellipse
intersecté par l’élément réfléchissant ; lorsque
l’ellipse est entièrement incluse dans les limites
de l’obstacle on a w=1 pour un élément de petite
taille par rapport à l’ellipse w tend vers zéro.
For a reflecting obstacle of finite dimensions, the
Fresnel ellipse is constructed from the position of the
receiver and the image of the source with respect to the
infinite surface embedding the obstacle. The Fresnel
ellipse is defined as the region of the plane for which:
dist S, X
(
)
+
dist X ,R
(
)
<
dist S,R
(
)
+
n .
The reflection is weighted by a factor w
i
=S
i
/
S
FZ
corresponding to the fraction of the ellipse
intersected by the reflecting element; when the
ellipse falls entirely inside the limits of the obstacle,
one has w=1, when the element is small compared
to the size of the ellipse w tends towards zero.

