Page 32 - base

Spécial “ 5es Assises sonore ”31
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : effets atmosphériques
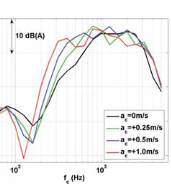
cas de l’atmosphère homogène. Les résultats de la figure 11
correspondent à des conditions de propagation favorables :
les niveaux acoustiques sont légèrement plus forts que dans
le cas de l’atmosphère homogène, et les spectres montrent un
décalage du creux d’interférences vers les basses fréquences
lorsque ac augmente, ce qui traduit une modification de l’effet
de sol.
Conclusion
Dans cet article, nous avons présenté quelques évolutions
récentes des modèles de propagation acoustique dans
la prise en compte des effets atmosphériques. Dans le
domaine fréquentiel, les modèles basés sur l’équation
parabolique permettent de considérer des environnements
de propagation complexe : propagation au-dessus d’un sol
inhomogène et/ou non plan, prise en compte des effets
de réfraction de façon précise (formulation MW-WAPE),
prise en compte des effets de diffusion par la turbulence
atmosphérique. Dans le domaine temporel, les méthodes de
résolution des équations d’Euler linéarisées par différences
finies sont de plus en plus utilisées pour la propagation
acoustique en milieu extérieur, même si ces méthodes
sont coûteuses en temps de calcul pour des distances de
propagation importantes. Elles sont particulièrement bien
adaptées au rayonnement de bruit large bande dans une
atmosphère inhomogène et en mouvement. Elles peuvent
également permettre d’obtenir des solutions de référence
pour le rayonnement acoustique des sources en mouvement,
dans le contexte du bruit des transports.
Dans les prochaines années, on peut penser obtenir des
avancées importantes en explorant les possibilités de
couplage entre modèles. On a présenté dans cet article des
résultats de couplage entre des modèles de propagation
acoustique et des modèles atmosphériques : ces modèles
couplés permettent de prédire les effets atmosphériques dans
des configurations complexes. On peut aussi mentionner la
possibilité de coupler un modèle de propagation temporel,
très précis en champ acoustique proche, à un modèle de
propagation fréquentiel de type EP, qui est mieux adapté à la
propagation sur de longues distances.
Références bibliographiques
[1] M.C. Bérengier, B. Gauvreau, Ph. Blanc-Benon, D. Juvé, Outdoor sound
propagation : A short review on analytical and numerical approaches, Acta
Acustica united with Acustica 89, 980-991 (2003).
[2] J. Defrance, M. Baulac, P. Jean, E. Premat : Modélisation de la propagation
acoustique en milieu extérieur complexe : effets de frontière, Acoustique &
Techniques 51 (2007).
[3] Ph. Blanc-Benon, L. Dallois, D. Juvé, Long range sound propagation in a
turbulent atmosphere within the parabolic approximation, Acta Acustica united
with Acustica 87, 659-669 (2001).
[4] E.M. Salomons, R. Blumrich, D. Heimann, Eulerian time-domain model for
sound propagation over a finite-impedance ground surface. Comparison with
frequency-domain models, Acta Acustica united with Acustica 88, 483-492 (2002).
[5] D. Heimann, R. Blumrich, Time-domain simulations of sound propagation
through screen-induced turbulence, Applied Acoust. 65, 561-582 (2004).
[6] D.K. Wilson, S.L. Collier, V.E. Ostashev, D.F. Aldridge, N.P. Symons, D.H.
Marlin, Time-domain modeling of the acoustic impedance of porous surfaces,
Acta Acustica united with Acustica 92, 965-975 (2006).
[7] B. Lihoreau, B. Gauvreau, M. Bérengier, Ph. Blanc-Benon, I. Calmet, Outdoor
sound propagation modeling in realistic environments : Application of coupled
parabolic and atmopsheric models, J. Acoust. Soc. Am. 120, 110-119 (2006).
[8] N. Blairon, Effets de la topographie sur la propagation des ondes acoustiques
dans l’atmopshère : modélisation avec l’équation parabolique et validation sur
site extérieur, thèse de doctorat, École Centrale de Lyon (2002).
[9] R.B. Stull, An Introduction to Boundary Layer Meteorology, Kluwer Academic (1988).
[10] D.K. Wilson, E.L. Andreas, J.W. Weatherly, C.L. Pettit, E.G. Patton,
P.P. Sullivan, Characterization of uncertainty in outdoor sound propagation
predictions, J. Acoust. Soc. Am. 121, EL177-183 (2007).
[11] S. Dupont, Y. Brunet, Simulation of turbulent flow in an urban forested park
damaged by a windstorm, Boundary-Layer Meteorology 120, 133-161 (2006).
[12] Site Internet de Meso-NH, http://mesonh.aero.obs-mip.fr/mesonh/.
[13] Ph. Blanc-Benon, D. Juvé, M. Karweit, G. Comte-Bellot, Simulation
numérique de la propagation des ondes acoustiques à travers une turbulence
cinématique, Journal d’Acoustique 3, 1-8 (1990).
[14] D. Juvé, Ph. Blanc-Benon, K. Wert, Numerical simulation of sound
propagation through time-dependent random media, Proceedings of Theoretical
and Computational Acoustics ’97, 653-665 (1997).
[15] B. Cotté, Ph. Blanc-Benon, Estimates of the relevant turbulent scales for
acoustic propagation in an upward refracting atmosphere, Acta Acustica united
with Acustica, accepté (2007).
[16] F. Junker, B. Gauvreau, Ph. Blanc-Benon, C. Cremezi-Charlet, D. Ecotière, O.
Baume, B. Cotté, Classification de l’influence relative des paramètres physiques
affectant les conditions de propagation à grande distance, rapport final convention
MEDD 18B/2003 (2006).
F. Junker, B. Gauvreau, Ph. Blanc-Benon, C. Cremezi-Charlet, Classification de
l’influence relative des paramètres physiques affectant les conditions de propagation
à grande distance, Acoustique & Techniques 39, 8-16 (2004).
[17] B. Cotté, Ph. Blanc-Benon, C. Cremezi-Charlet, F. Poisson, Modélisation de la
propagation acoustique à moyenne distance du bruit des trains à grande vitesse,
18ème Congrès Français de Mécanique, 27-31 août, Grenoble (2007). ■
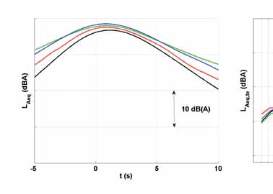
Fig. 11 : Propagation du bruit de TGV à 300 m en conditions favorables, à l’aide du modèle de sources équivalentes
couplé à un code EP : signatures temporelles (gauche) et spectres en tiers d’octave (droite)