Page 30 - base

Spécial “ 5es Assises sonore ”29
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : effets atmosphériques
Néanmoins, Heimann et Blumrich [5] ont montré la faisabilité
d’une telle approche ; à l’aide d’un modèle de turbulence
simple, ils ont étudié la propagation acoustique à travers un
écoulement instationnaire derrière un écran acoustique.
Même si les modèles de propagation acoustique actuels
sont capables de prendre en compte la diffusion des
ondes acoustiques par la turbulence atmosphérique, il faut
insister sur la complexité des phénomènes à modéliser.
Tout d’abord, il existe une différence importante entre les
fluctuations turbulentes de température, qui est une grandeur
scalaire, et les fluctuations turbulentes de vitesse, qui est
une grandeur vectorielle. Ces deux types de fluctuations
ont des spectres et des propriétés de diffusion différents ;
l’équation parabolique MW-WAPE peut être utilisée pour
étudier numériquement ces différences [3,15]. D’autre
part, les hypothèses d’homogénéité et d’isotropie de la
turbulence, qui sont couramment utilisées, ne sont pas
toujours vérifiées dans la couche limite atmosphérique, en
particulier pour les grandes tailles de structures turbulentes.
Enfin, il est important de comprendre quelles sont les tailles
de structures turbulentes à modéliser lorsqu’on réalise un
calcul de propagation acoustique dans une atmosphère
turbulente. En effet, les échelles spatiales caractéristiques
des fluctuations turbulentes dans l’atmosphère couvrent
un domaine très important, s’échelonnant du millimètre au
kilomètre. Certaines tailles de structures turbulentes ont un
effet de diffusion plus important que d’autres : il y a donc une
sélection des tailles de fluctuations turbulentes qui s’effectue,
sélection qui dépend de la fréquence acoustique et de la
géométrie de propagation considérées [15]. Il est important
de comprendre ce couplage entre la fréquence acoustique,
la géométrie de propagation et les échelles turbulentes à
considérer pour modéliser la propagation acoustique dans
une atmosphère turbulente.
Spécificités du bruit des transports
Dans cette partie, on s’intéresse à plusieurs caractéristiques
du bruit des transports, et à la façon dont ils peuvent être pris
en compte dans les modèles numériques. Tout d’abord, le bruit
des transports, comme le bruit industriel, est souvent un bruit
large bande, caractérisé par un spectre en tiers d’octave [16].
Avec les modèles fréquentiels de propagation, il est possible
d’obtenir des résultats en tiers d’octave en réalisant plusieurs
calculs monofréquentiels par tiers d’octave [16]. La
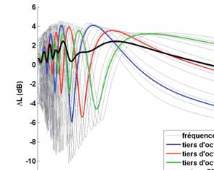
figure 8 permet de comparer le niveau de pression
par rapport au champ libre calculé sur l’octave 500 Hz,
sur les tiers d’octave composant l’octave 500 Hz, et
pour différentes fréquences pures dans l’octave 500 Hz
(4 calculs monofréquentiels par tiers d’octave). En
augmentant la largeur de bande, les interférences dues
à l’effet de sol se trouvent lissées.
Une autre spécificité du bruit des transports est le
mouvement de la source. Les modèles temporels
de propagation sont bien adaptés pour considérer le
rayonnement acoustique d’une source en mouvement.
Un exemple simple est présenté dans la figure 9, où on
considère le rayonnement acoustique d’une impulsion
gaussienne au repos au-dessus d’un sol rigide, dans
un écoulement uniforme. Cette configuration est
équivalente, par changement de repère galiléen, au
rayonnement d’une impulsion gaussienne en mouvement
rectiligne uniforme au-dessus d’un sol rigide, dans une
atmosphère au repos. A t = 0, le champ de pression est
représenté par une distribution spatiale gaussienne. La
figure 9 montre le champ de pression à des temps ultérieurs,
pour un écoulement uniforme orienté vers la droite de nombre
de Mach M = 0,5.
Le mouvement de la source peut également être pris en
compte à l’aide d’un modèle de sources équivalentes. Dans ce
type de modèle, des sources au repos fictives sont distribuées
le long de la trajectoire de la source acoustique. Le niveau
de pression au récepteur est calculé pour l’ensemble de ces
sources fictives, et la signature temporelle est obtenue en
considérant les temps de propagation entre les sources fictives
et le récepteur. Les modèles de sources équivalentes peuvent
également être utilisés dans des situations où la source ne
peut pas être considérée comme compacte, comme pour le
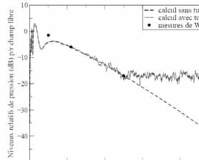
Fig. 7 : Niveau de pression par rapport au champ libre dans
une zone d’ombre acoustique, calculé avec et sans
turbulence. Paramètres des calculs : f = 424 Hz,
hS = 3,7 m, hR = 1,5 m, ac = -0,5 m/s, sol herbeux
Fig. 8 : Influence de la largeur de bande du signal : calculs
monofréquentiels, en tiers d’octave et en octave du niveau
de pression par rapport au champ libre. Paramètres des
calculs : hS = 5 m, h R = 2 m, a c = 0, sol herbeux