Page 29 - base

28
Spécial “ 5es Assises sonore ”
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : effets atmosphériques
comme Méso-NH [12], peuvent couvrir une région entière
(échelle de l’ordre du kilomètre), mais ne sont pas (encore)
très précis dans les très basses couches de l’atmosphère,
i.e. à l’échelle métrique ; c’est ce type de modèle qu’utilisent
Wilson et al. [10] comme donnée d’entrée de leur code EP.
Les modèles atmosphériques existants doivent donc être
raffinées et adaptés pour pouvoir être couplés à un modèle
de propagation acoustique.
Influence des fluctuations turbulentes dans
l’atmosphère : effets de diffusion
Les variations rapides de température et de vitesse de vent
autour de leur valeur moyenne sont appelées fluctuations
turbulentes. Ces fluctuations ont un effet de diffusion sur
les ondes acoustiques, effet qui est particulièrement visible
en présence d’une zone d’ombre acoustique (c’est-à-dire
pour des conditions de propagation dites défavorables,
ou derrière un relief ou un écran acoustique). La figure 6
montre des cartographies du niveau de pression sur le tiers
d’octave 800 Hz, calculées à l’aide d’un code EP avec et sans
turbulence. Le niveau sur le tiers d’octave 800 Hz est obtenu
à partir de 5 calculs monofréquentiels. La zone d’ombre
acoustique, clairement visible dans le cas sans turbulence,
est générée en utilisant un profil de célérité logarithmique avec
un fort gradient vertical (ac = -2,1 m/s). Dans le cas où des
fluctuations turbulentes de température sont présentes, les
niveaux acoustiques sont plus élevés dans la zone d’ombre.
Pour prendre en compte l’effet des fluctuations turbulentes
dans un modèle de propagation acoustique, deux approches
peuvent être envisagées. La première consiste à synthétiser
différentes réalisations de la turbulence (champs turbulents
de température et/ou de vitesse), qui sont utilisées comme
données d’entrée d’un modèle de propagation acoustique. La
valeur moyenne de la pression est ensuite calculée à partir
des résultats des différentes réalisations. Cette approche
fait appel à l’hypothèse de turbulence gelée : le temps de
propagation de l’onde acoustique est supposé beaucoup
plus court que le temps caractéristique des fluctuations
turbulentes. La deuxième approche consiste à synthétiser
une turbulence transitoire dans un modèle temporel de
propagation acoustique. Une source acoustique continue est
utilisée, et le temps de simulation est pris bien supérieur au
temps caractéristique des fluctuations turbulentes.
Les résultats de la figure 6 sont obtenus en suivant la
première approche ; 30 réalisations de la turbulence sont
synthétisées à l’aide d’une méthode de modes de Fourier
aléatoires [3,13], qui permet d’obtenir des champs turbulents
avec une distribution spectrale donnée (spectre de von Kármán
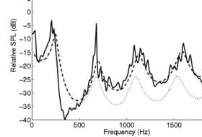
ici). Cette méthode a été validée par comparaison avec des
données expérimentales, comme le montre la figure 7 [8]. Juvé
et al. [14] ont montré que cette méthode pouvait être étendue
au cas d’une turbulence dynamique, en couplant un code EP
tridimensionnel à un code de mécanique des fluides basé
sur la simulation des grandes échelles (LES). La deuxième
approche, où une turbulence transitoire est synthétisée, est
difficile à appliquer en pratique car les modèles temporels de
propagation sont très coûteux en temps de calcul, et qu’une
telle approche suppose des temps de simulation importants.
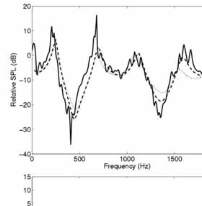
Fig. 5 : Spectre du niveau de pression par rapport au champ
libre pour M1 à 25 m (en haut), et pour M4 à 75 m (en
bas) : comparaison entre les résultats expérimentaux
(trait continu) et les simulations MW-WAPE/SUBMESO
(en tirets). La courbe en pointillés correspond aux
simulations WAPE pour une atmosphère homogène
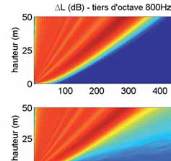
Fig. 6 : Cartographie du niveau de pression par rapport
au champ libre sur le tiers d’octave 800 Hz sans
turbulence (haut), et avec une turbulence synthétisée
par une méthode de modes de Fourier aléatoires
(bas) ; hS = 2 m, a c = -2,1 m/s, sol herbeux