Page 28 - base

Spécial “ 5es Assises sonore ”27
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : effets atmosphériques
On notera dans l’article hS la hauteur de la source et hR la
hauteur du récepteur ; ici hS = hR = 2 m. Les résultats de la
figure 2 sont tracés en terme de niveau de pression relatif
au champ libre : ΔL = L - LCL, avec L le niveau de pression
de la configuration étudiée, et LCL le niveau de pression en
champ libre dans une atmosphère homogène. Les résultats
du calcul MW-WAPE sont en très bon accord avec les
mesures sur l’ensemble du spectre de fréquences. Avec
le calcul WAPE, les interférences sont moins bien prédites
aux hautes fréquences. Pour obtenir ces bons résultats
numériques, il faut bien noter qu’une description précise
de la topographie, de l’impédance du sol et des conditions
atmosphériques a été nécessaire. Lorsque des mesures
de bruit dans l’environnement sont réalisées en pratique, il
est difficile d’avoir accès à une description aussi précise de
l’environnement de propagation.
Les profils logarithmiques ne permettent pas toujours d’estimer
les profils de température et de vent dans l’atmosphère de
façon satisfaisante. Au-dessus d’un sol plat et homogène,
il est possible d’utiliser la théorie de la similitude de Monin-
Obukhov pour obtenir ces profils dans la couche de surface
de l’atmosphère, dont la hauteur est approximativement un
dixième de la hauteur de la couche limite atmosphérique [9]. La
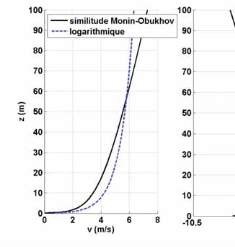
figure 3 permet de comparer les profils calculés avec la théorie
de la similitude de Monin-Obukhov aux profils logarithmiques
pour une atmosphère stable (les paramètres de la théorie de
la similitude pour ces profils sont pris dans [10]).
Pour des configurations plus complexes, et en particulier en
présence de reliefs ou d’obstacles, il est nécessaire d’avoir
recours à un modèle atmosphérique pour obtenir les profils
verticaux de température et de vent. Récemment, plusieurs
études ont montré qu’il était possible de coupler un modèle
de propagation acoustique, en l’occurrence un code EP, à un
modèle atmosphérique [7,10]. Lihoreau et al. [7] utilisent un
modèle micrométéorologique appelé SUBMESO, basé sur une
résolution des équations de conservation de la mécanique des
fluides à l’aide d’une simulation des grandes échelles (LES)
et d’une technique d’emboîtement de domaines. Ce modèle
permet de calculer les composantes du vent dans les trois
directions et la température à l’échelle du site (19 km x 19 km).
Leur étude porte sur le site expérimental permanent du LCPC
(« Station de Long Terme » de Saint-Berthevin), traversé par
une vallée d’une profondeur moyenne
de 35 mètres (voir également le site
Internet du LCPC : http://www.lcpc.
fr/fr/presentation/moyens/slt/). La
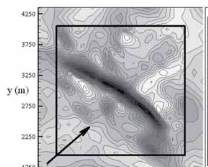
figure 4 permet de visualiser le champ
de vitesse calculé par SUBMESO à une
hauteur de 5 m au-dessus du sol, pour
une période de stratification neutre de
l’atmosphère (sans effets thermiques) ;
la résolution horizontale est de 50 m.
La vitesse du vent est plus faible au
niveau de la vallée, et plus forte au
niveau des reliefs. A partir de ces
résultats, Lihoreau et al. [7] obtiennent
des profils moyens de température
et de vitesse de vent qu’ils utilisent
comme données d’entrée du code
MW-WAPE. La figure 5 montre que
les résultats du modèle MW-WAPE/
SUBMESO sont en bon accord avec
les résultats expérimentaux.
Les résultats présentés par Lihoreau
et al. [7] sont prometteurs. Toutefois,
le modèle atmosphérique SUBMESO
présente certaines limitations : il suppose l’atmosphère
neutre, et il ne prend pas en compte correctement les bilans
énergétiques près du sol. D’autres modèles météorologiques
ont été développés récemment, qui permettent d’obtenir une
description précise de l’atmosphère à des échelles spatiales
données. Certains modèles, comme AQUILON [11], sont
très précis à l’échelle locale (de l’ordre du mètre), mais ne
prennent pas en compte les conditions atmosphériques à
l’échelle régionale (atmosphère supposée neutre). D’autres,
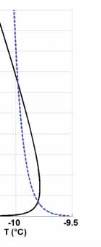
Fig. 3 : Profils verticaux de vitesse de vent (gauche) et de température (droite) pour
une atmosphère stable : comparaison entre les profils calculés avec la théorie
de la similitude de Monin-Obukhov (vitesse de friction de 0, 28 m/s et échelle de
température de -0,04 K) et les profils logarithmiques (aϖ = 0,92 m/s et aT = -0,08 K)
Fig. 4 : Cartographie horizontale du champ de vitesse de vent
en m/s calculé par le modèle SUBMESO à une hauteur de
5 m. La flèche noire indique la direction du vent moyen