Version HTML de base

26
Spécial “ 5es Assises sonore ”
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : effets atmosphériques
de célérité effective de forme arbitraire. Par ailleurs, des
équations paraboliques approchées ont été développées à
partir des équations de la mécanique des fluides, permettant
de prendre en compte le champ de vitesse explicitement [3].
Parmi celles-ci, on peut mentionner la formulation MW-WAPE
(pour Mean Wind Wide-Angle Parabolic Equation), d’ordre deux
en nombre de Mach M = v/c
0
, qui sera utilisée dans la suite
de l’article.
Depuis quelques années, les méthodes temporelles de
propagation acoustique connaissent un essor important [4,5,6],
avec l’accès de plus en plus facile à des puissances de calcul
élevés. Celles-ci sont basées sur une résolution des équations
d’Euler linéarisées par différences finies, et permettent de
prendre en compte les effets atmosphériques de façon précise.
Elles sont particulièrement bien adaptées à la propagation
du bruit large bande. Néanmoins, ces méthodes temporelles
sont très coûteuses en temps de calcul, ce qui rend difficile
l’étude de configurations sur de longues distances, et/ou de
configurations tridimensionnelles. De plus, la prise en compte
d’un sol d’impédance finie n’est pas directe [4,6]. En effet, les
modèles d’impédance de sol classiquement utilisés pour la
propagation acoustique en milieu extérieur ont été développés
dans le domaine fréquentiel, et ne sont généralement pas de
nature causale.
Dans cet article, nous présenterons des résultats numériques
récents obtenus soit à l’aide de l’équation parabolique dans
le domaine fréquentiel, soit à l’aide des équations d’Euler
linéarisées dans le domaine temporel, pour illustrer les effets
de réfraction et de diffusion des ondes acoustiques par
l’atmosphère. Nous montrerons également comment certaines
spécificités du bruit des transports, tel le mouvement de la
source, peuvent être modélisées.
Influence des conditions atmosphériques
moyennes : effets de réfraction
En première approximation, les profils moyens de température
et de vent près du sol peuvent être assimilés à des profils
logarithmiques :
( )
(
)
0
0
1ln
zz
a T zT
T
+
+ =
,
( )
(
)
0
1ln
zz
a zv
v
+
=
,
avec z
0
la longueur de rugosité, qui varie entre 1 et 10 cm
en milieu extérieur, et T
0
la température à la hauteur z
0
. Avec
l’équation parabolique de type WAPE, ces profils sont pris en
compte à travers la célérité effective, qui s’écrit alors [7] :
( )
(
)
0
0
1ln
zz
a c z c
c
eff
+
+ =
.
Avec l’équation parabolique de type MW-WAPE, par contre,
ces profils peuvent être directement inclus dans le calcul.
Lihoreau et al. [7] comparent les résultats de ces deux
types d’équation parabolique à des résultats expérimentaux
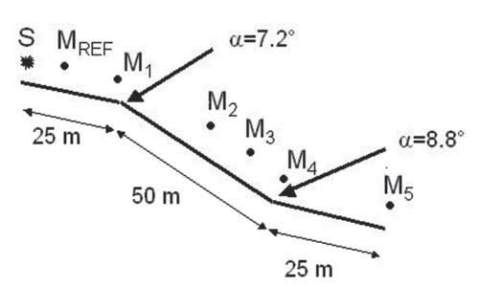
dans un environnement de propagation complexe, dont la
géométrie est donnée sur la figure 1. Pour prendre en compte
la topographie du site, le domaine de calcul est divisé en trois
sous-domaines où le sol est supposé plan, en utilisant une
technique proposée par Blairon [8]. L’impédance du sol est
estimée expérimentalement ; elle n’est pas homogène entre
la source et le microphone M5 [7].
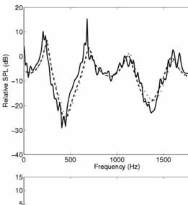
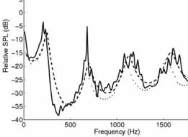
Les résultats numériques sont comparés aux mesures sur la
figure 2 pour les microphones M
1
et M
4
, à, respectivement,
25 m et 75 m de la source. Pour ces mesures, les paramètres
des profils logarithmiques, sont : a
T
= 0,20 K, a
ϖ
= 0,65 m/s,
θ
= 20°, soit a
c
= 0,73 m/s pour le profil de célérité effective
utilisé dans le calcul WAPE.
Fig. 1 : Dispositif expérimental sur le site du
LCPC près de Saint-Berthevin
Fig. 2 : Spectre du niveau de pression par rapport au
champ libre pour M
1
à 25 m (en haut), et pour M
4
à 75 m (en bas) : comparaison entre les résultats
expérimentaux (trait continu) et les simulations
EP (WAPE en pointillés et MW-WAPE en tirets)

