Version HTML de base
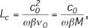
46
Spécial “ Acoustique sous-marine ”
Acoustique
&
Techniques n° 48
Partant d’un profil sinusoïdal, le raidissement de la zone
de transition entre surpression et dépression ne cesse de
s’accentuer au cours de la propagation sur une distance
caractéristique dite longueur de formation de l’onde
de choc L
c
. Intuitivement, cette distance correspond
à peu près au parcours nécessaire pour que les zones
de surpression et dépression se décalent d’un quart de
longueur d’onde
λ
:
où
ω
représente la pulsation de l’onde et M =
ν
0
/c
0
le
nombre de Mach. Cette distance est ainsi d’autant plus
courte que le niveau de l’onde est élevé ou que la fréquence
est grande. Du fait du caractère cumulatif du phénomène,
la transformation vers une allure en dent de scie devrait
être toujours observable, mais après propagation sur
une distance plus ou moins longue, pour une onde
plane dans un milieu non absorbant. Ce sont en fait les
phénomènes de diffraction du rayonnement combinés à
l’effet de l’absorption qui limitent la manifestation de la
non linéarité.
L’atténuation des ondes acoustiques dans l’eau de mer
est due à la viscosité du milieu et à des phénomènes
de relaxation (transition de molécules entre états
différents). A une fréquence donnée, on peut la
caractériser par la longueur de propagation L
α
pour
laquelle l’amplitude de l’onde est divisée par e = 2,7.
L’atténuation d’une onde est d’autant plus grande que la
fréquence de l’onde est élevée. Le tableau 1 reproduit
quelques valeurs typiques.
Tabl. 1 : Atténuation pour différentes fréquences
Le comportement de l’onde dépend du rapport de ces
deux distances, donné par le nombre de Gol’dberg
Γ
= L
α
/L
c
-
Γ
< 1 : L’onde est atténuée avant d’être déformée : il n’est
alors pas nécessaire de tenir compte des phénomènes
non-linéaires.
-
Γ
> 1 : le niveau de l’onde est tel que celle-ci se déforme
significativement avant d’être atténuée. La modélisation
doit prendre en compte les développements au deuxième
ordre.
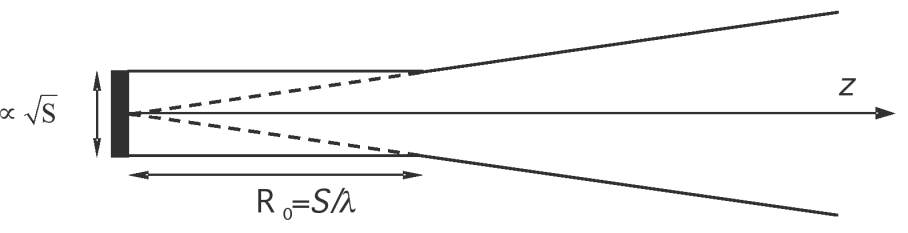
Le rayonnement d’une antenne dépend aussi du
phénomène de diffraction lié aux dimensions de l’antenne
par rapport à la longueur d’onde. Il est caractérisé par
la distance de Fraunhofer R
0
(Figure 2). Pour simplifier,
on peut supposer qu’en deçà de cette distance (champ
proche), la propagation est unidimensionnelle. Au-delà
(champ lointain), elle obéit à la divergence sphérique et
l’amplitude de l’onde décroît inversement à la distance.
La distance de Fraunhofer intervient donc comme la
longueur d’atténuation, et notamment les effets non
linéaires sont négligeables si cette distance est beaucoup
plus faible que la longueur de formation de l’onde de
choc.
Les trois longueurs introduites ci-dessus apparaissent
explicitement
dans
l’approximation
parabolique
généralement utilisée pour modéliser le rayonnement non
linéaire d’une antenne directive.
L’équation KZK établie par Kuznetsov, Zabolotskaya et
Khokhlov (1969-71) s’écrit ainsi :
D
S
W
W
A
w
w
w
w
w
w
³
2
2
2
0
1
1
1
4
c
t
u
u
u
u
u
z
L
L
*
diffraction
terme non linéaire
atténuation
où la vitesse acoustique est définie par la quantité sans
dimension u =
ν
/
ν
0
, l’axe de propagation principal est z,
les axes transverses sont adimensionnés à la longueur
caractéristique de l’antenne, et la grandeur
τ/ω
= t-z/c
0
est le temps retardé.
(
est l’opérateur gradient appliqué aux directions
transverses du rayonnement). On retrouve l’équation de
propagation linéaire en négligeant le dernier terme.
Fig. 2 : Modèle simplifié de la diffraction d’une onde émise par une pupille de surface S
Utilisation de la non-linéarité de la propagation en acoustique sous-marine

