Page 46 - base

Spécial “ Acoustique sous-marine ”45
Acoustique
&
Techniques n° 48
Propagation non-linéaire et longueurs
caractéristiques
Dans une grande variété de problèmes et applications,
on peut admettre que la propagation acoustique obéit
à une équation linéaire : une onde plane harmonique ne
se déforme pas au cours de sa propagation ; seule son
amplitude décroît à cause de l’atténuation. L’équation de
propagation linéaire est obtenue avec des développements
au premier ordre (Euler,1755), en considérant que les
différentes grandeurs physiques caractérisant le milieu
(pression, densité…) ne subissent que des petites
perturbations. En revanche, des phénomènes non-
linéaires apparaissent quand ces perturbations sont plus
importantes. Il faut alors utiliser des développements
à l’ordre supérieur pour modéliser correctement la
propagation (Earnshaw et Riemann,1860).
La non-linéarité peut s’interpréter comme une variation locale
Δc de la vitesse de propagation acoustique (célérité c0)
dans le milieu sous l’effet du passage d’une onde. Deux
phénomènes sont à l’origine de cette variation : la
convection et les propriétés thermodynamiques du milieu
(équation d’état). Le premier phénomène procède d’une
simple composition de vitesses, où la vitesse acoustique
(vitesse particulaire) v s’additionne localement à la célérité −
l’onde se "porte", soit Δc 1 = v. La dépendance de la célérité
avec la pression est à l’origine du second phénomène : la
fluctuation de célérité correspondante est proportionnelle
à la variation de pression (pression acoustique) p induite
par la présence de l’onde, soit Δc 2 ∝(1)p. La variation
totale de la célérité locale est donc la somme de ces deux
contributions. Elle s’exprime dans le cas d’une onde plane
− où p ∝ v − en fonction de la seule vitesse acoustique par
la relation Δc = Δc1 + Δc2 = βv β est le coefficient de
non-linéarité, qui est de 3,5 pour l’eau de mer.
Pour fixer les ordres de grandeur, considérons une
perturbation acoustique de l’ordre de 1 bar (105Pa soit
220 dB ref 1µPa (2)), c’est-à-dire une onde relativement
intense. La variation correspondante de célérité est de
l’ordre de Δc = 0,2 m/s, à comparer à la valeur nominale
c 0 = 1 500 m/s. La variation de célérité reste donc faible
en valeur relative. L’explication qui suit montre que l’effet
de cette faible variation peut se développer au cours de
la propagation et devenir ainsi, au terme d’un processus
cumulatif, manifestement observable.
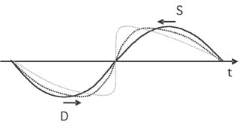
Considérons une onde plane d’allure sinusoïdale
dont l’amplitude de vitesse acoustique est notée ν0
(Figure 1). La célérité c = c 0+βν0 dans la zone de
surpression notée S est plus grande que celle c=c 0 - βν0
dans la zone de dépression notée D. La perturbation se
propage donc plus rapidement en S qu’en D. L’écart
entre ces zones diminuant, le signal se déforme vers
une allure en dent de scie.
Utilisation de la non-linéarité de la
propagation en acoustique sous-marine
Jacques Marchal, Pierre Cervenka
Laboratoire de Mécanique Physique CNRS FRE 2867
Université Pierre et Marie Curie
2, place de la gare de ceinture
78210 Saint Cyr l’Ecole
Tél.: 01 30 85 48 00
Fax : 01 30 85 48 99
E-mail : jmarchal@ccr.jussieu.fr
Résumé
Cet article donne des bases intuitives sur les mécanismes de la non-
linéarité de la propagation. Le principe de l’émission paramétrique est
exposé avec le modèle de Westervelt. Dans le domaine sous-marin, ce
type d’émission trouve essentiellement son application avec les sondeurs
profileurs de sédiment. On mentionne finalement un projet visant à la
détection d’objets enfouis.
Abstract
This paper exposes several intuitive clues about the mechanism of
nonlinear propagation. The principle of parametric transmission is exposed
through the Westervelt model. In the underwater domain, this kind of
transmission is mostly applied with sediment echo-sounder systems.
À current research project that is devoted to buried object detection is
described.
Fig. 1 : Déformation d’une onde au cours de sa propagation
1- ∝ = proportionnel à
2- 220 dB ref 1µPa = 220 dB référencé 1 microPascal