Version HTML de base
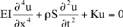
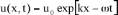
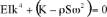
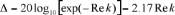
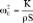
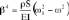
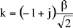
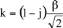
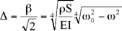
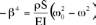
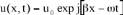
26
Acoustique
&
Techniques n° 46-47
L’équation différentielle de la flèche u de la poutre suivant y,
en un point d’abscisse x, est alors :
Ensuite, le rail étant un milieu étendu (« infini »), il apparaît
pertinent de considérer une modélisation de ses vibrations
sous forme d’une superposition d’ondes et de chercher les
solutions sous la forme :
,
où k est le nombre d’onde et
ω
la pulsation de l’onde.
La relation de dispersion des ondes s’écrit :
et le taux de décroissance de l’onde dans le rail est introduit
sous la forme :
,
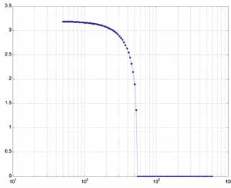
on obtient la courbe (Fig. 8) de taux de décroissance de l’onde
dans le rail suivante, pour un modèle de voie très simplifié :
Il faut alors distinguer deux cas suivant le signe de (K-
ρ
S
ω
2
),
soit en notant :
,
et suivant les valeurs relatives de
ω
par rapport à
ω
0 :
Si
ω
<
ω
0, l’équation de dispersion devient k
4
+
β
4
=0, avec
,
et les solutions physiques (non-croissance exponentielle de
l’onde à l’infini) sont :
- Pour x>0 :
- Pour x<0 :
Le nombre d’onde a une partie réelle non nulle, ce qui
correspond à une onde évanescente non-amortie : on se
trouve dans une « bande interdite » pour la propagation des
ondes et le taux de décroissance s’écrit :
Si
ω
>
ω
0, l’équation de dispersion devient k
4
-
β
4
=0, avec
,
et les solutions physiques (non-croissance exponentielle de
l’onde à l’infini) sont :
- Pour x>0 :k=j
β
- Pour x<0 : k=-j
β
On obtient une solution :
,
c’est-à-dire une onde sinusoïdale propagative sans atténuation.
On se trouve dans une bande passante pour la propagation
avec un taux de décroissance
Δ
=0.
La frontière bande interdite/bande passante est la pulsation
de résonance du rail sur son appui.
La figure 8 est représentative des phénomènes de propagation
des ondes dans le rail si on ne considère que le rail et la
semelle sous rail. Nous verrons que RODEL nous fournit un
taux de décroissance plus complet et plus représentatif du
comportement global de la voie. On y retrouve cette allure
simplifiée de taux de décroissance avec la notion de bande
interdite/bande passante limitée par une résonance du rail
sur son appui.
Courbes expérimentales et mécanismes physiques
Accélérance
Expérimentalement, la réponse vibratoire de la voie va être
obtenue par la mesure de l’accélérance à poste fixe. On la
mesure à l’aide d’une excitation au marteau d’impact et de la
réponse vibratoire d’un accéléromètre positionné sur le rail.
Les fonctions de réponse en fréquence verticales et latérales
ainsi que les cohérences correspondantes entre accélérations
et force d’excitation sont mesurées dans une gamme de
fréquences comprises entre 50 et 6 400 Hz et moyennées
sur une dizaine de chocs.
En exemple sur la figure 9 : deux accélérances verticales
mesurées sur chaque file de rail auxquelles on a superposé
la simulation sous RODEL de la réponse du rail seul et de la
réponse de la traverse seule.
Fig. 8 : Taux de décroissance verticale de la modélisation
simplifiée voie/poutre sur appuis élastiques continus
Caractérisation vibro-acoustique
d’une voie ferrée
Approfondissons…

