Version HTML de base
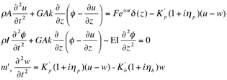
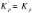
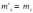
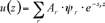
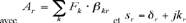
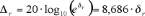

25
Acoustique
&
Techniques n° 46-47
Pour modéliser le comportement vibratoire de cette voie, le
lien entre la réponse vibratoire du rail, issue d’une excitation
au point de contact roue/rail, et son rayonnement acoustique
peut être exprimé de manière simple et analytique dans le
domaine fréquentiel à partir de la modélisation mise en œuvre
dans TWINS (Fig. 5) [6], [7].
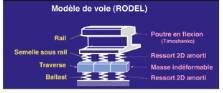
Prenons, par exemple, dans TWINS, RODEL qui modélise la
voie sur la base de quelques hypothèses simplificatrices :
- le rail est considéré comme une structure de type poutre
à section indéformable le long de laquelle se propagent des
ondes vibratoires ;
- les traverses et le ballast constituent un appui linéique ;
- le système d’attaches et le ballast sont considérés comme
des raideurs 2D amorties.
Avec les deux premières hypothèses, 4 types d’ondes vont
se propager dans le rail :
- une onde verticale propagative,
- une onde verticale évanescente,
- une onde latérale propagative,
- une onde latérale évanescente.
Si on repart des équations de base régissant le bruit de
roulement (Cf. Manuel Théorique de TWINS 3.0) avec :
Les équations de mouvement s’écrivent alors sous la forme :
avec
/ (distance entre 2 traverses) et
/
(distance entre 2 traverses)
Et le déplacement transversal u (z) de la section du rail
supposée indéformable s’écrit sous la forme :
Fk : force d’excitation dans la direction k
β
kr : réceptance partielle de l’onde r dans la direction k
Ar : amplitude de la réponse vibratoire pour l’onde r
ψ
r : déformée modale de l’onde r
sr : nombre d’onde complexe de l’onde r
(kr caractérise la propagation de l ’onde,
δ
r son
atténuation)
Pour déterminer u(z), il suffit de connaître l’amplitude
des vibrations au point de contact (reliée à l’accélérance)
et l’atténuation de l’onde dans le rail reliée au taux de
décroissance. On introduit ci-dessous l’expression du taux
de décroissance que nous allons expliciter par la suite.
Partant de ces formulations, nous verrons qu’il est envisageable
de limiter la puissance acoustique rayonnée par la voie soit en
spécifiant des valeurs limites pour le taux de décroissance des
ondes dans le rail, soit en imposant des paramètres de voie
particuliers (type de rail, type de traverse, type de semelle
sous rail).
Propagation des ondes dans le rail : introduction et
définition du taux de décroissance
Avec les modèles de voie présentés précédemment et
appliqués dans TWINS, le taux de décroissance introduit
n’a pas une expression simple. On propose de partir d’une
modélisation simplifiée pour mieux expliciter et aborder les
phénomènes physiques mis en jeu.
Considérons une poutre mince (Bernoulli-Euler) droite en flexion
verticale (x,y) sur appuis élastiques de raideur K uniformément
répartis (poutre de Winkler), de module d’Young E, d’inertie I
et de masse linéique
ρ
S, le long de laquelle va se propager
des ondes vibratoires.
Fig. 5 : Modèle de voie simplifié issu de TWINS
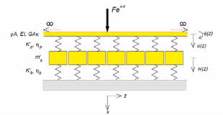
Fig. 6 : Modélisation de la voie : type poutre sur support continu
Fig. 7 : Modélisation simplifiée de la voie : poutre
sur appuis élastiques continus
Caractérisation vibro-acoustique
d’une voie ferrée
Approfondissons…

