Version HTML de base

8
e
CFA - Tours 2006
31
Acoustique
&
Techniques n° 45
on obtient le variogramme expérimental. Pour obtenir une
expression analytique facilement utilisable, ce variogramme
est ensuite approché par une fonction mathématique. Cette
fonction décrit la structure de corrélation de la fonction
aléatoire Z qui modélise d’un point de vue probabiliste notre
variable d’étude z.
Le variogramme est une fonction croissante avec jusqu’à
une distance limite appelée portée à partir de laquelle il
se stabilise à un niveau de palier. La portée caractérise la
distance d’influence des points de mesure. Au-delà de cette
distance les mesures ne sont plus corrélées.
Krigeage
La méthode d’interpolation en géostatistique est le krigeage
(appelé ainsi en hommage au Docteur Donald Krige pour
ses travaux sur les gisements d’or en Afrique du Sud). Il se
définit comme le meilleur estimateur linéaire et sans biais
de la fonction aléatoire Z. Il est une combinaison linéaire
des données. Son critère de qualité (ou d’optimalité) est la
minimisation de la variance de l’erreur d’estimation. Cette
variance se calcule avec le variogramme. Les pondérateurs
dépendent ainsi de la forme de la fonction mathématique
ajustée au variogramme expérimental.
Application au champ des propriétés de sol
Le krigeage a été tout d’abord appliqué au cas plus simple
où l’on peut supposer que la variable est stationnaire d’ordre
2, c’est-à-dire que sa moyenne et sa variance ne dépendent
pas de la position dans l’espace. Le champ acoustique n’a pas
de telles propriétés puisqu’il dépend largement de l’expansion
du front d’onde. Par contre, les mesures dans le cadre de
la campagne de 2005 avaient été effectuées au-dessus
d’un terrain plan homogène dont les propriétés acoustiques
semblaient
a priori
stationnaires. La Figure 3 présente le
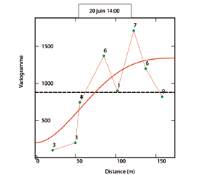
variogramme expérimental et la fonctionmathématique ajustée
pour les mesures d’impédance du 20 juin à 14 heures traduites
en paramètres phénoménologiques: la résistance spécifique
au passage de l’air du modèle de Delany et Bazley ([2] et
[3]). Tout d’abord nous nous sommes imposés de prendre en
compte les incertitudes expérimentales évaluées à 20 cgs
pour ce type de sol. Celles-ci correspondent à un bruit blanc
traduit sur un variogramme par une discontinuité à l’origine.
Le variogramme expérimental est ensuite ajusté selon une
fonction dont la portée est de 186 mètres. L’ajustement peut
sembler approximatif, néanmoins le faible nombre de points
de mesures rend nécessairement le variogramme erratique
et sa modélisation quelque peu arbitraire.
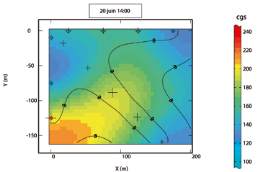
Après modélisation de l’autocorrélation des données de
résistivité, nous avons réalisé une interpolation par krigeage
aboutissant à la carte de la Figure 4. Le sens d’une carte de
krigeage est de montrer les valeurs d’interpolation ayant la
plus forte probabilité d’être proche de la vraie valeur. Les
contraintes imposées dans le système de calcul du krigeage
lui donnent cet aspect lissé. La lecture d’une telle carte est
complétée par l’information de l’écart-type de krigeage. Cet
écart-type nous informe sur l’erreur d’estimation des valeurs en
chaque point de la maille interpolée. Le résultat que l’on peut
observer satisfait l’idée selon laquelle les propriétés du sol
sont plutôt continues mais avec des zones plus absorbantes
que d’autres.
Application au champ acoustique
Nous avons également appliqué les méthodes géostatistiques
aux données acoustiques. Afin de nous affranchir des
effets liés à la directivité de la source et aux fluctuations de
puissance d’émission, nous avons réalisé une transformation
du niveau brut mesuré en niveau d’atténuation par rapport aux
microphones de référence placés à 10 mètres de la source
pour chacune des directions de propagation (Figure 1). Dans
le cas du champ acoustique, le phénomène étudié présente
une forte tendance non-stationnaire due principalement à
la divergence géométrique. Une méthode géostatistique
permettant de prendre en compte ce type de phénomènes
est appelée krigeage universel.
Cette méthode introduit une fonction de dérive
modélisant la tendance de non stationnarité. La fonction
aléatoire
que l’on cherche à estimer est alors une
superposition de la dérive et d’une composante aléatoire de
Apport des méthodes géostatistiques à l’estimation de l’impact acoustique d’une source en environnement ouvert
Fig. 3 : Variogramme expérimental et modèle ajusté
d’autocorrélation (courbe en gras) pour les mesures de
résistivité spécifique au passage du site de mesures de
Lannemezan – le nombre de paires de points utilisés pour
le calcul est rappelé pour chacune des classes de distance.
La ligne horizontale indique la demie-variance des données
Fig. 4 : Carte de résistivité spécifique au passage de l’air obtenue
par krigeage et isolignes de l’écart-type d’erreur d’estimation.
Les points de mesure sont indiqués par des croix

