Version HTML de base
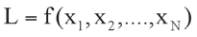

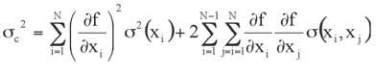
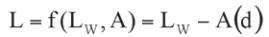
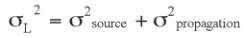
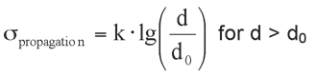
“Uncertainty-noise” Le Mans
35
Acoustique
&
Techniques n° 40
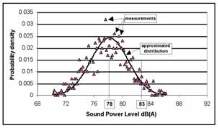
In our example this level that is not exceeded by a confidence
of 95 % is 83 dB(A).
In many cases the level L is not measured – or predicted –
directly, but is determined fromN other quantities x
1
, x
2
, ….,x
N
through a functional relationship
(2)
If the uncertainty of these quantities can be characterized by
the standard deviations
σ
1
,
σ
2
…
σ
N
, the combined uncertainty
σ
c
of the level L to be determined can be expressed as
(3)
This is true if the input quantities xi are uncorrelated. If some
or all of these input quantities are correlated, the appropriate
expression is
(4)
Here the covariance
σ
(x
i
, x
j
) expresses the correlation between
x
i
and x
j
.
These are the basics. The combined uncertainty
σ
c
as it shall
be used in all measurement standards is an excellent concept
to quantify the different influences on the uncertainty of the
result – there is no reason why the same concept should not
be used in the prediction of sound pressure levels.
In prediction we have some – often not very precise –
information about the partial steps, but only very rough and
often no knowledge about the accuracy of the final result.
Taking into account that noise mapping is a financially
interesting business, we should not be content if different
groups declare their results to be the most accurate ones. A
sober analysis based on scientific principles is the best way
to tackle the problem.
The concept of uncertainty
in noise prediction
If we want to characterise the result of a noise prediction
calculation by an uncertainty, we have first to clarify what this
end result shall be.
The basic element or “atom” of all predictions is the calculation
of the sound pressure level L in a distance d of a simple omni
directional and with all energy in one frequency band radiating
point source. The result can be expressed as
(5)
where L
W
is the sound power level of the source and A(d) is
the combined attenuation caused by many influences. If we
know the uncertainty of the source emission
σ
-
source
and of the
propagation calculation
σ
-
propagation
, the combined uncertainty
resulting from (3) and (5) is
(6)
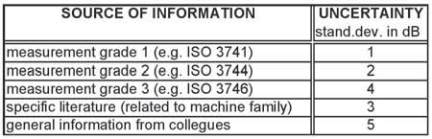
The uncertainty of the sound power level of the source
depends on the method used to determine it. In our old –
pre-GUM- concept the relevant standards are characterised
by the grade 1, 2 or 3 and these grades define the maximal
standard deviation of the population of all possible results if
this standard is applied.
Table 1 : Examples of uncertainties of source emission
σ
-
source
The uncertainty in propagation calculation
σ
-
propagation
depends
on the method used. From comparisons measurement-
calculation and based on reports from colleagues we
recommend to use as first approximation (as long as there is
a lack of more precise knowledge)
(7)
with d
0
=10 m and k = 2 dB.
The so defined standard deviation increases from 0 dB at 0
m – 10 m to 2 dB at 100 m and 4 dB at 1000 m. It is only a
rough assumption based on the use of traditional models in
Europe (e.g. ISO 9613-2) and should be updated and more
detailed step by step.
Uncertainties in the prediction of environmental noise and in noise mapping
Fig. 1 : Dispersed results of sound power measurements
and approximation by a normal distribution

