Version HTML de base
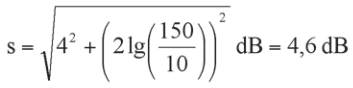

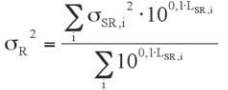

36
“Uncertainty-noise” Le Mans
Acoustique
&
Techniques n° 40
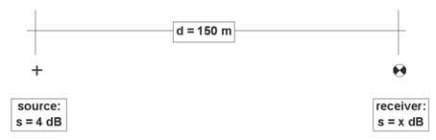
If we calculate the sound pressure level caused by a source
with an uncertainty of the assumed emission of 4 dB in a
distance of 150 m we get an uncertainty of the predicted
sound pressure level of
(8)
Generally the calculated sound pressure level at the receiver
is the energetic sum of many contributions. If we calculate
with frequency spectra or if more sources contribute to the
receiver level – in all these cases we can calculate for each
contribution the partial level and its uncertainty.
Applying (3) on the equation for level summation
(9)
we get the uncertainty
σ
R of the calculated level at the
receiver
(10)
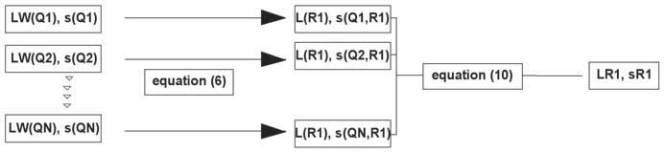
Equation (10) allows to integrate the concept of uncertainty in
prediction calculations and in noise mapping. It is even possible
to calculate noise maps with levels of a certain confidence.
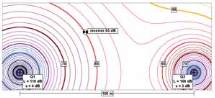
The principle is shown in Figure 3.
This procedure is an approximation – in reality the propagation
uncertainties of all the contributing sources are not completely
uncorrelated. But without any further knowledge this is the
best assumption.
Determination of uncertainties with noise maps
This procedure cannot only be used for defined receivers, but
also for complete noise maps. This is shown with figures 4 –
6. Figure 4 shows the noise map calculated with ISO 9613-2.
The sound power level of source Q1 is estimated and therefore
the standard uncertainty is assumed to be 4 dB, while this
standard deviation may be 3 dB for source Q2. Based on the
procedure figure 3, the uncertainty of the whole calculation
is determined and presented as “uncertainty map” in figure
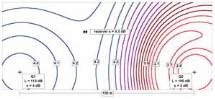
5. Adding these two maps figures 4 and 5 with a coverage
factor 1,65 for a one sided confidence of 95 %, the map figure
6 was calculated. It shows the levels, that are not exceeded
with a probability of 95 %.
Extended sources
are generally split in
subparts so small
that these can be
i nc l uded i n t he
calculation like point
sources. This creates
a l ittle problem –
if we calculate the
uncertainty of the
receiver level from
one source with emission L
W
and uncertainty s or we have
two sources with emission (L
W
– 3 dB) and uncertainty s each
the uncertainty of the result will be smaller in the latter case.
This is because the applied equation (10) is only valid for
Fig.2 : Sound propagation from one
elementary point source to receiver
Fig. 3 : Determination of the uncertainty of the calculated noise level at receiver R1 from sources Q1 – QN
Fig. 4 : Noise map calculated with ISO 9613-2
Fig. 5 : Total uncertainty of the predicted receiver
level and it’s spatial distribution
Fig. 6 : Map of noise levels not to be exceeded
with confidence 95 %.
Uncertainties in the prediction of environmental noise and in noise mapping

