Version HTML de base
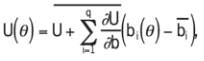
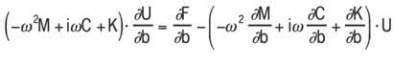
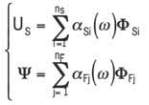
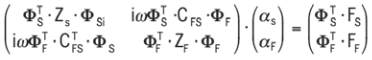
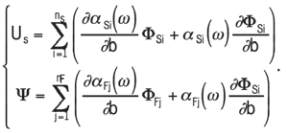
28
“Uncertainty-noise” Le Mans
Acoustique
&
Techniques n° 40
Monte-Carlo simulation
Solving this system of equations for a relatively high number
of realizations of the random design variables leads to a
sampling of the nodal values of the unknown potentials and
displacements. Post-processing operations can then be
applied to these basic values in order to get samples of local
response indicators (such as the pressure field) or of global
indicators (such as the mean quadratic pressure over the
domain). Statistical convergence properties guarantee that
applying statistical operators to the produced samples gives
estimates of the parameters of the response distribution
laws. It is however difficult, for industrial problems, to obtain
(even low order) converged statistics due to the high number
of repeated simulations. In addition to poor convergence
properties, Monte-Carlo simulation suffers from the following
drawbacks:
- in the context of high variability level (where alternative
non-deterministic methods are not efficient), a significant
dependence of the response distribution law on the parameter
distribution law is possible;
- no error estimates are available to investigate the accuracy
of the computed response statistics.
Sensitivity analysis and perturbation approach
in physical coordinates
The perturbation SFEM basically assumes that the random
vibro-acoustic response can be represented by a first-order
Taylor development in the neighbourhood of the mean
configuration:
(3)
By first-order differentiating Eq. (2) with respect to a given
parameter b, the following relation is obtained:
(4)
with the quantities
K
,
C
,
M
,
U
and
F
being evaluated at the
nominal value of b. This relation shows that the first-order
sensitivity of the unknown potentials and displacements can
also be evaluated by solving a complex-valued algebraic
system. It is noticeable that this system has the same operator
as the zeroth-order system, which drastically reduces the
computational effort required for the solution (as the system
already exists in factorised form). The right-hand side of the
first-order algebraic system involves the sensitivities of the
K
,
C
,
M
matrices and of the excitation
F
with respect to the
design parameter b.
Applying first-order and second-order statistical operators to
the approached response surface directly leads the mean
and variance of the response indicators. Statistics of post-
processing fields can be obtained similarly. It is clear that
the global accuracy achieved by the perturbation SFEM
depends on 1) the variability level of the design variables and
2) the nonlinearity degree of the implicit relation between the
response indicator and the design variables [2].
Sensitivity analysis and perturbation approach in
modal coordinates
The solution strategy in physical coordinates (direct approach)
described above should be distinguished from a modal
approach in which the eigenmodes of the system (and their
associated sensitivities) are first identified and used as a base
for developing the unknown response (and its associated
sensitivities). Referring to the previously-stated linear vibro-
acoustic problem in the frequency domain, the structural and
acoustic eigenmodes, (
ω
Si
,
Φ
Si
) (i=1,…,n
S
) and (
ω
Fj
,
Φ
Fj
) (j=1,…
,n
F
) resp., are extracted prior to the frequency analysis. The
unknown potentials and displacements can then be projected
on their respective modal bases:
(5)
and the modal coordinates are obtained at each discrete
frequency by solving the following system of equations of
order n
S
+n
F
:
(6)
Observe that, due to the convergence properties of the modal
superposition, the low-frequency range analysis does not
require a full extraction of the eigenmodes of the structure
and the fluid domain. A reduction of the problem dimension is
consequently achieved in this way.
For first-order sensitivity analysis, the modal superposition
is first-order differentiated, which leads to the following
relations:
(7)

