Version HTML de base
8
Characterisation of sound absorbing materials
Porosity can be evaluated with commercial equipment
(picnometer), based on the measurement of pressure
variations as a result of small volume variations in a small
cavity or methods derived from this [6]. A few years ago,
an elegant method has been proposed to extract the poro-
sity from the high frequency selection coefficient of the
sample. In the asymptotic limit of the high frequencies,
the reflection coefficient of a thick sample depends only
on tortuosity and porosity [7,8].
The measurement of the flow resistivity is well described
in ISO 9053:1991. An (low frequency) AC and a DC method
are described. Since the acoustic behaviour of the material
at low frequencies is dominated by the viscous effects, the
flow resistivity can also be extracted from the transmission
coefficient of the sample at very low frequencies [9].
For a long time, the tortuosity was evaluated by measuring
the electrical conducting liquid. The more «tortuous» the
pores, the higher the electrical resistivity. The method was
developed for geological samples (see for instance the refe-
rences on this subject in [1]) and was not always easy to
apply this method to plastic foams. Fifteen years ago, Allars
[10] proposed a simple method to evaluate the tortuosity
from the high frequency asymptotic behaviour of the phase
velocity of the acoustic slow wave in the material.
At high frequencies, the inertia of the frame is too large
and the frame remains immobile, as if the material was
rigid. The only wave that can propagate is the air wave. At
high frequencies, the viscous skin depth is very small and
viscosity does not influence the velocity very much. The
compressibility is basically adiabatic and the only parame-
ter influencing the phase velocity at these frequencies is
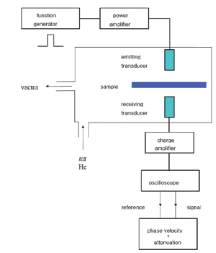
the inertia and thus the tortuosity. The experimental set
up is shown in Figure 1.
Special air-coupled (piezoelectric or capacitive) transdu-
cers are used to emit and detect high frequency sound
waves in air. The phase velocity is determined as a func-
tion of frequency by unwrapping the phase of the Fourier
Transform of the received pulse.
The viscous and the thermal characteristic lenghts are
without any doubt the most difficult to measure among
the acoustic parameters. They determine the transition
between low and high frequencies velocity profile in the
pores and between isothermal and adiabatic compression
of the air in the pores respectively. Since viscous effects
are dominant in small constrictions in the pores and ther-
mal effects are more dependent on the average distance
the heat has to travel to reach the pore walls, two diffe-
rent characteristic pore sizes are needed, the «viscous»
pore size being always smaller or equal to the «thermal»
pore size. These characteristic pore sizes can be estima-
ted (at least in order of magnitude) from the attenuation
of an ultrasonic wave that passes through the material. If
discrimination between viscous and thermal characteris-
tic length is needed, the attenuation should be measured
with different gases (having different viscous and thermal
properties) saturating the pores [11].
This is schematically shown in figure 1, where the set-up
is build in a transparent container, that can be filled with
helium or air. For details on the measurement of
L
and
L′
,
see the references [1] and [2].
Mechanical parameters
If the flow resistivity of the material is not too high and if
the material is not in contact with a vibrating plate, the
acoustic parameters suffice to describe the acoustic beha-
viour of the material. In all other cases, the mechanical
parameters are also needed. Techniques to measure the
elastic coefficients of soft materials exist (Oberst type
experiments) but regarding poro-elastic materials, some
supplementary complications occur :
- The coupling between air and frame introduces some extra
attenuation, that is not a result of the frame’s damping. The
experiments should be performed in vacuum or the inver-
sion should take the coupling with the air into account.
- Since the materials are often designed to have a maxi-
mum damping in the audio frequency range, the principle
of causality shows that this results in a frequency depen-
dent elastic modulus.
- Due to the manufacturing process (foam rising or fibrous
material build-up), the mechanical parameters (and often
to a lesser extend also the acoustic parameters) become
anisotropic. In most cases, an orthotropic symmetry descri-
bes the material accurately, but it requires the introduc-
tion of supplementary elastic coefficients.
- The elastic coefficients of materials used in acoustic
applications may vary from 10
5
Pa to 10
9
Pa. This enor-
mous range makes it difficult to design one single experi-
ment that can measure this entire range.
A typical set-up for the measurement of the shear modu-
lus is shown in Figure 2. A shear wave is generated in
two slabs of the porous material (using a shaker attached
to a plate). From the position and the width of the reso-
nance peak, the shear storage and loss modulus can be
determined.
Fig. 1 : Experimental set-up for the ultrasonic
measurement of the tortuosity (from ref [3])

