Version HTML de base
10
Characterisation of sound absorbing materials
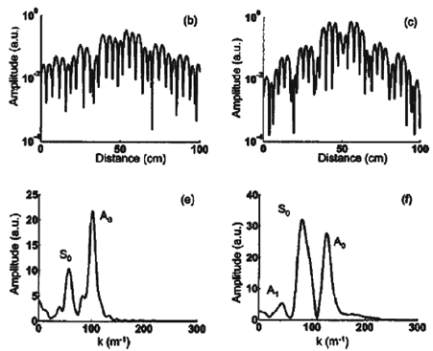
Fig. 6 : Standing wave pattern and spatial Fourier
Transform for the configuration of figure 5.
Frequency 66 Hz (left) and 800 Hz (right)
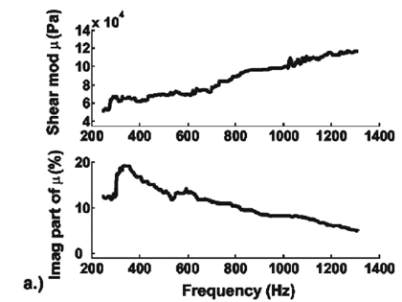
By fitting the theoretical dispersion curves to the measured
ones, the shear modulus as a function of frequency can
be extracted. Figure 7 shows a typical result of a shear
modulus of a foam as a function of frequency.
At present, work is continuing on different configurations
that are more easy to realise and on the temperature
dependence of the elastic constants.
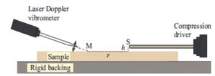
A «simplified» version of this technique has been proposed
by Geebelen [17]. Using an acoustic point source made
of a compression driver and a tube, a shear wave can be
generated in a layer of the sample. The quarter wavelenght
resonance of this shear wave can be detected with a laser
Doppler vibrometer pointing at an angle towards the surface.
This method does not require a complicated set-up.
Fig. 8 : Experimental set-up for measuring the shear modulus from
the quarter wavelenght resonance in a layer (from ref [16])
Conclusion
An overview has been presented of the different methods
that can be used to determine the material parameters
that govern the acoustic behaviour of a poro-elastic mate-
rial. It is now possible to obtain the frequency dependent
shear modulus for vibroelastic foams.
Remerciements
This manuscript describes the activities during the last
fifteen year at the «Laboratory foe Acoustics and Thermal
Physics» of the K.U. Leuven, Leuven, Belgium. This work
would not have been possible without the contribution of
numerous doctoral students, postdocs and visitors.
Bibliography
[1] JF. Allard, N. Attala «Propagation of sound in porous media», Wiley, (2009)
[2] TE. Vigran «Building Acoustics», Taylor and Francis, (2008)
[3] W. Lauriks and P. Leclaire, «Materials testing» in «Handbook of signal
processing in acoustics» ed. David Havelock, Sonoko Kuwano and Michael
Vorländer, Springer New York, (2008)
[4] C. Zwikker, CW. Kosten, «Sound absorbing materials», Elsevier, (1949)
[5] http://apmr.matelys.com/index.html
[6] P. Leclaire, O. Umnova, K. Horoshenkov, «Porosity measurements by comparing
air volumes», Review of scientific instruments 74 (2003) pp 1366-1370.
[7] Z. Fellah, S. Berger, W. Lauriks, C. Depollier, P. Trompette, Y. Chapelon,
«Ultrasonic measurement of the porosity and tortuosity of air-saturated random
packings of beads», Journal of Applied Physics 94, pp 9352-9359
[8] F. Fellah, S. Berger, W. Lauriks, C. Depollier, M. Fellah, «Measuring the porosity
of porous materials having a rigid frame via reflected waves : A time domain
analysis with fractional derivatives», Journal of Applied Physics, 93-1 pp 296-303
[9] N. Sebaan Z. Fellah, W. Lauriks, C. Depollier, «Measuring flow resistivity of
porous material via acoustic reflected waves», Journal of Applied Physics, 98-8
[10] JF Allard, B. Castagnède, M. Henry, W. Lauriks, «Evaluation of tortuosity in
acoustic porous materials saturated by air».
[11] P. Leclaire, L. Kelders, W. Lauriks, C. Glorieux, J. Thoen, «Determination
of the viscous characteristic length in air-filled porous materials by ultrasonic
attenuation measurements», JASA, 99-4, pp 1944-1948
[12] W. Sachsen Y. Pao, «On the determination of phase and group velocities of
dispersive waves in solids» Journal of Applied Physics, 49 (1978) pp. 4320-4327
[13] http://www.noe.co.jp/en/product/pdt3/mat/mat05.html
[14] L. Boeckx, P. Leclaire, P. Khurana, C. Glorieux, W. Lauriks, J. Thoen,
«Investigation of the phase velocities of guided acoustic waves in soft porous
layers», JASA, 117 (2005) pp 545-554
[15] C. Glorieux, W. Gao, S. Kruger, K. Venderostyne, W. Lauriks, J. Thoen,
«Surface acoustic depth profiling of elastically inhomogeneous materials»,
Journal of Applied Physics 88 (2000) pp 4394-4400
[16] L. Boeckx, P. Leclaire, P. Khurana, C. Glorieux, W. Lauriks, JF. Allard,
«Guided elastic waves in porous materials saturated by air under Lamb
conditions», Journal of Applied Physics 97, 094911 (2005)
[17] N. Geebelen, L. Boeckx, G. Vermeir, W. Lauriks, JF. Allard, O.Dazel,
«Measurement of the rigidity coefficients of a Melamine foam», Acta Acustica
united with Acustica 93 (2007) pp 783-788
Fig. 7 : Typical result of a shear modulus as a function of frequency

