Version HTML de base
35
Le découplage de structures à l’aide d’isolateurs passifs
Prise en compte des non-linéarités
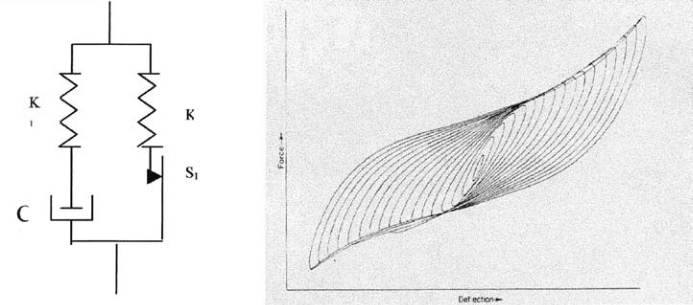
On fait appel à un agencement de modèles simples
comme le Standard Triboelastic Sol id pour traduire
l ’élasticité combinée au frot tement sec complété par
un dash-pot pour traduire l ’ef fet de viscosité.
Certains auteurs préfèrent considérer des raideurs varia-
bles plutôt que d’avoir à multiplier le nombre d’éléments.
On peut également faire appel à une représentation du
cycle d’hystérésis à l’aide des modèles de Dahl, Duhem-
Madelung, de Bouc, ou encore comme A. Al Majid et R.
Dufour considérer un modèle plus général de la relation
force de restitution/déformation qui rende compte de
manière plus satisfaisante du comportement en environ-
nement vibratoire fait de superpositions de différents
types d’excitation.
Ces approchent sont prometteuses et donnent déjà d’ex-
cellents résultats.
Conclusion
La dé nition de la suspension ou du découplage vibra-
toire de structures fait partie intégrante du travail de
conception. En tant qu’interface entre des structures
son coût et sa performance en dépendent de façon
telle qu’il faut la considérer comme une étape a pren-
dre en compte au début du projet.
Le meilleur compromis coût/performance peut être appro-
ché grâce à la panoplie de plots qu’offre le marché ou par
des moyens de conception renforcés par des outils de
prédiction des performances de plus en plus ables.
L’approche non-linéaire par les cycles d’hystérésis est promet-
teuse. Elle va progressivement permettre d’orienter puis
ef cacement les recherches. Sur les matériaux, les géomé-
trie et les travaux sur des plots encore plus évolués.
Avertissement
Cet article est tiré du numéro 25 d’Acoustique & Techniques.
Ce numéro avait été publié dans le cadre du 1
er
Forum
européen sur les matériaux insonorisants qui s’est tenu au
CETIM, Senlis le 3 juillet 2001. Ce numéro spécial est dispo-
nible en téléchargement sur le site http://www.bruit.fr
Références bibliographiques
[1] Budzdugan G., Dynamique des fondations de machines, Ed Eyrolles.
[2] Skudrzyk E, Simple and complex vibratory systems, The Pennsylvania state
university press.
{3] Ferry JD, Viscoelastic properties of polymers, John Wiley & sons. Inc
[3] Freakley PK, Payne AR, Theory and practice of engineering with rubber,
Applied science publishers.
[4] Julien MA, Dynamique des systèmes pendulaires,Technip.
[5] VerheÏj JW, Multi-path sound transfer from resiliently mountod shipboard
machinery, Institute of applied physics tno-th.
[6] Harris and Crede , Shock and vibration handbook, Mc Graw-Hill Book Company.
[7] Soula M., Etude du comportement mécanique des matériaux viscoélastiques
par les dérivées fractionnaires, Thèse de doctorat, CNAM, Paris.
[8] Al Majid A., Dufour R, Colloque Vibrations, Chocs et Bruit , Mécanique
industrielle et matériaux, revue du GAMI Juin 1998
[9] Lazutkin AM, Description of an arbitrary multi-axial loading process for
non-linear vibration isolators, 111anov G.V., Academic Press Limited
[10] Gjika K., Dufour R., Ferraris G., Transient response of structures on
viscoelastic mounts prediction and experiment, LMS URA CNRS 862 INSA Lyon.
1996 Academic Press Limited
[11] Ko JM, Ni YQ, Tian QL, Hysteresis behavior and empirical modeling of v~ire-
cable vibration isolator, Hong-Kong Polytechnic. The international Journal of
analytical and experimental modal analysis vol. 7 n° 2 p 11-127, Avril 1992.
[12] Bliman PA, Etude mathématique d’un modèle de frottement sec : le modèle
de P.R. Dahl, Thèse Université Paris IX ; mars 1990.
[13] Hepbum C. et Reynolds RJW., Elastomers : criteria for engineering design.
Applied Science Publishers.
[14] Snowdon JC., Vibration and shock in damped mechanical systems, John
Wiley& Sons.
[15] Lalanne M., Berthier P., Der Hagopian J., Mécanique des vibrations
linéaires, Masson.
[16] Lalanne C., Vibrations et chocs mécaniques, Hermes
[17] Bouc R., Modèle mathématique d’hystérésis, Thèse de doctorat, CNRS AO 3078
[18] Werely NM., MadLavan V., Sieg T., Mechanism-based analysis of thermo-
mechanical elastomeric lag damper behavior, American Helicopter Society,
Forum 1999.
[19] Baber TT., Noori MN., Modeling general hysteresis behavior and random
vibration application, J. of Vibration, Acoustics, Stress and Reliability in Desing 1986.
[20] Table ronde MV2 06-1996 ; Un modèle forcé de restitution pour prévoir les
réponses à des chocs d’une structure montée sur des plots à friction.
[21] Pompéi, Génie mécanique des caoutchoucs. Exemples de dimensionnement :
calcul et tolérance des raideurs., Ed C G’Sell - A. Coupard-Apollor.
[22] Levallard P., Caractérisation rhéologique des ferro uides sous champ
magnétique-Application aux supports hydrauliques, Thèse LMMM-ESAM, 1990.
[23] Ramrakhyani DS., Brackbill CR., Lesieutre GA., Smith EC., Non Iinear
Modeling of Elastomeric Materials for Helicopter Dampers, Rubber Division,
American Chemical Society. 17-20 oct 2000
[24] Leif Karj., Structure-Borne Sound Properties of Vibration Isolators. Doctoral
thesis 1998, Royal Institute of Technology MWL Stockholm.
Fig. 18 : Exemple de modèle et de cycle d’hystérésis d’un plot en caoutchouc naturel

