Version HTML de base
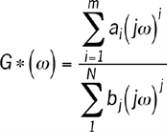
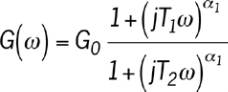
34
Le découplage de structures à l’aide d’isolateurs passifs
Le comportement linéaire suppose que ces modules sont
constants en fonction de l’amplitude.
Ces deux méthodes donnent les valeurs des termes des
matrices pour chaque fréquence. Il faut conserver ces
valeurs sous forme numérique pour pouvoir exploiter les
matrices. Pour éviter ce stockage, il est commode d’es-
sayer de trouver des modèles analogiques simples à partir
de composants élémentaires.
Les modèles analogiques
L’agencement des éléments simples doit donner un modèle
dont le comportement traduit assez dèlement la réalité.
Les plus utilisés sont les modèles de Kelvin, Voigt-Maxwell
et Zener. On peut utiliser des combinaisons de ces modè-
les pour parfaire la représentation du comportement par
exemple introduire des masses pour faire apparaître l’effet
de l’inertie de la matière. Quand on ne fait pas intervenir
la masse de la matière on peut appliquer cette modélisa-
tion tout aussi bien au plot qu’au matériau.
A l’aide d’un modèle généralisé de Voigt-Maxwell ou de Kelvin
on peut théoriquement traduire le comportement rhéologi-
que du matériau. Ceci revient à lier l’effort à la déformation
par deux opérateurs différentiels linéaires. Ceci conduit
en régime harmonique au module complexe du matériau
(respectivement à la raideur complexe du plot).
Cette forme présente quelques problèmes d’exploita-
tion numérique quand m et n sont grands. Dans le but de
réduire le nombre de paramètres, Hue et Vinh ont proposé
une formulation aux dérivées fractionnaires.
Cette dernière prenant en compte les valeurs de la fonc-
tion à tous les instants du passé peut rendre compte de
l’effet mémoire du matériau.
Cette formulation n’est pas d’utilisation courante pour le
moment, car il paraît plus urgent de prendre en compte les
non-linéarités dont les effets sont plus préoccupants que
ceux de la fréquence dans beaucoup de domaines.
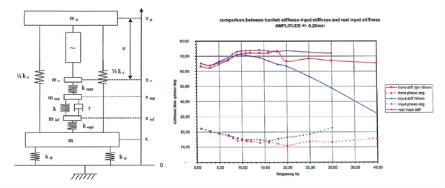
Fig. 16 : Modèle analogique de la machine de mesure. Exemple de résultats de mesure de raideurs et d’amortissements
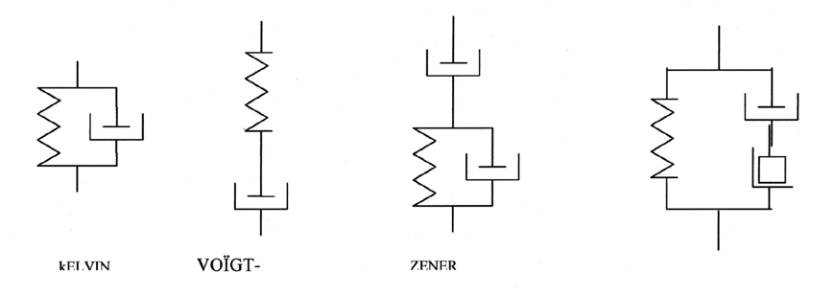
Fig. 17 : Les modèle analogiques
KELVIN
VOÏGHT-MAXWELL
ZENER
COMBINAISON DES MODÈLES

