Version HTML de base
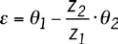
17
Mesure haute précision de vitesse angulaire instantanée pour la surveillance et la caractérisation d’excitation en machine tournante
Mesure de l’Erreur de Transmission
ou du déphasage angulaire
L’Erreur de Transmission est reconnue comme étant la prin-
cipale source d’excitation des transmissions de puissance
synchrones (engrenages, chaînes, courroies). Dans ces
mécanismes, elle est définie théoriquement comme la diffé-
rence entre la position réelle de la roue et la position qu’elle
aurait occupée si l’engrenage avait été parfait (sans défor-
mation, avec une cinématique parfaite de la développante de
cercle). Une définition équivalente et plus «matérielle» peut
être donnée par l’écart entre les positions angulaires des
deux roues d’engrenage au rapport de réduction près :
(1)
avec z
1
et z
2
les nombres de dents de l’organe menant
et de l’organe mené,
θ
1
et
θ
2
les positions angulaires des
arbres correspondants. Elle peut être généralisée comme
un déphasage angulaire entre les deux arbres liés par l’en-
grenage. Dans le cas particulier d’une mesure à l’aide de
deux codeurs placés aux extrémités d’un même arbre solli-
cité en torsion, ce déphasage angulaire peut également
être assimilé à une déformation en torsion, permettant
ainsi de caractériser une vibration de torsion.
Principe de mesure du déphasage angulaire
La mesure de déphasage angulaire proposée repose sur une
méthode originale qui consiste à compter le nombre d’im-
pulsions délivrées par une horloge haute fréquence entre
deux événements du signal de chaque codeur (Voir figure 1).
Ces signaux sont des créneaux compatibles TTL et les événe-
ments déclenchant le comptage des impulsions de l’horloge
sont généralement les fronts montants des créneaux. Ce prin-
cipe de mesure revient donc à dater l’apparition d’événements
réputés être localisés angulairement à pas constant.
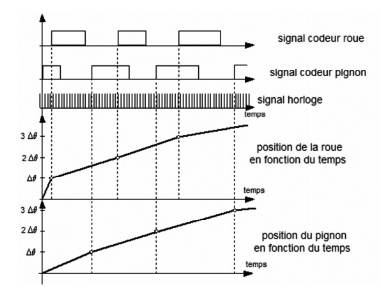
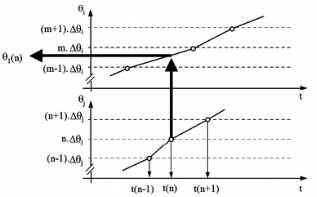
Fig. 1 : Principe de mesure de la position angulaire
de deux arbres à l’aide de codeurs optiques
L’horloge doit délivrer des impulsions à une fréquence la
plus élevée possible pour garantir une bonne précision. Ce
comptage s’effectue en simultané sur les deux voies avec la
même référence temporelle (même horloge et même comp-
teur) à l’aide d’une carte de comptage traditionnelle. Disposer
d’une référence temporelle commune donne accès simultané-
ment à l’écart entre les deux voies de mesure. Il est possible
ensuite de reconstruire la loi d’évolution de la position angu-
laire des arbres qui portent les codeurs optiques en fonc-
tion du temps et cela à une cadence donnée par le nombre
de raies sur chaque codeur. On obtient ainsi une dissocia-
tion de la résolution du codeur optique (nombre de points
de mesure par tour) et de la précision de mesure (essentiel-
lement caractérisée par la fréquence de l’horloge).
Intérêt de l’échantillonnage angulaire
Une manière naturelle de reconstruire l’Erreur de Transmission
à partir de ces positions angulaires consiste à échantillon-
ner à pas constant en temps les deux courbes obtenues
par interpolation. Dans ce cas, les points d’échantillonnage
temporels ne sont pas localisés à la même position angu-
laire d’un tour sur l’autre. Ce phénomène est lié à l’Erreur
de Transmission elle-même qui induit des fluctuations de
la vitesse de rotation. Par exemple, lorsqu’un défaut de
faux-rond devient substantiel, les points d’échantillonnage
bougent le long du profil de denture, conduisant alors à une
erreur causée par le processus d’échantillonnage. Il est
alors impossible de comparer la mesure réalisée d’un tour
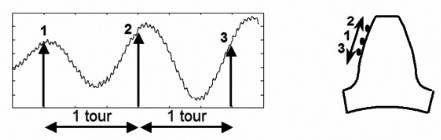
sur l’autre. La figure 2 accentue ce mouvement d’un point
d’échantillonnage le long du profil, d’un tour sur l’autre, pour
illustrer ce phénomène. De plus, un tour complet d’un arbre
est forcément approché par un multiple de pas d’échan-
tillonnage temporel, il est alors difficile d’obtenir précisé-
ment la périodicité d’un tour comme un multiple entier de
pas d’échantillonnage
Fig. 2 : Déplacement du point d’échantillonnage sur plusieurs
tours successifs pour un échantillonnage temporel
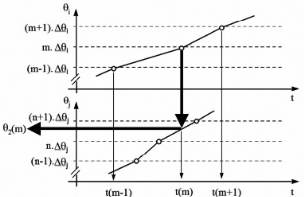
Dans le cas d’un échantillonnage angulaire, les points de
reconstruction de l’Erreur de Transmission coïncident avec
l’apparition d’un événement sur un signal codeur. Ainsi, on
parlera d’échantillonnage angulaire en référence à la voie
1 (figure 3(a)) ou en référence à la voie 2 (figure 3(b)).
Fig. 3 : Reconstruction des positions angulaires et construction de l’Erreur de Transmission
(a)
(b)

