Version HTML de base
44
Machines thermoacoustiques
mènes thermiques et le mode dit de «vorticité» (mode de
cisaillement, indice v sur la figure). Par suite, en particu-
lier, une composante normale de la vitesse particulaire
apparaît qui provient des processus de diffusions du
mouvement thermique et du mouvement de cisaillement
qui prennent naissance sur la paroi. Ainsi, par exemple,
la composante suivant l’axe «u» normal à la paroi (située
en u = s) de la vitesse particulaire totale
ν
u
(u) (indice «n»
sur la figure) est proportionnelle à la pression acousti-
que «p» et est donnée par l’équation (1) dans le cas d’un
mouvement harmonique :
€
v
u
u
( )
=
v
u
s
( )
+
k
0
r
w
2
k
0
2
1
k
v
ψ
v
−
ik
v
u
(
)
− ψ
v
−
ik
v
s
(
)
[
]
+ γ −
1
k
h
ψ
h
−
ik
h
u
(
)
− ψ −
k
h
s
(
)
[
]
ω
ρ
0
c
0
2
p
(1)
où les fonctions
ψ
v
(-ik
v
u) et
ψ
h
(-ik
h
u) représentent respec-
tivement le champ de vitesse de vorticité (v
v
) et le champ
de vitesse entropique (V
h
) qui tendent tous deux vers zéro
aux distances respectives
€
δ
v
=
2 k
v
et
€
δ
h
=
2 k
h
de la paroi (épaisseurs des couches limites visqueuse
et thermique), et où la somme des fonctions qui dépen-
dent de la coordonnée «s» représente le champ de
vitesse particulaire associé aux effets de viscosité,
de conduction thermique et acoustique sur la paroi
(ce dernier v
u
(s) étant nul sur une paroi rigide), k
0
→
w
représentant la composante tangentielle à la paroi du
nombre d’onde.
.
€
k
0
k
0
r
w
2
= −∆
r
w
(
)
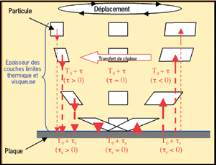
Fig. 1 : Mouvement d’une particule et flux de chaleur
(flèches rouges) au voisinage d’une paroi
Comme mentionné précédemment, ces couches limi -
tes agissent sur la réflexion du champ de vitesse parti -
culaire de la même manière qu’un matériau dissipatif et
réactif dont l’impédance serait finie. Mais de surcroît,
ces phénomènes qui se développent dans les couches
limites visqueuses et thermiques peuvent être exploi -
tés pour créer des phénomènes thermoacoustiques
conduisant à des applications en termes de machines
thermiques, réfrigérateurs, pompes à chaleur et géné-
rateurs (moteurs).
Le phénomène thermoacoustique
De façon classique, il est coutume de penser onde acous-
tique dans les gaz en termes de déplacement particulaire
et d’écart instantané de pression couplés l’un à l’autre.
Cependant, comme relaté ci-dessus, des oscillations de
température accompagnent toujours les oscillations de
pression (et de position). La combinaison de toutes ces
oscillations, et leur interaction avec les parois rigides,
compte tenu des effets visqueux et thermiques, sont à
l’origine de divers effets. Bien que ces effets soient trop
petits pour être perçus dans les applications courantes,
ils peuvent être exploités pour réaliser des machines ther-
miques (thermoacoustiques) performantes [9-14] ou des
systèmes thermoacoustiques utilisés à des fins de métro-
logie [6-8]. Les applications relevant de la thermoacousti-
que sont présentées au paragraphe 4 ci-dessous.
Lorsqu’une particule de fluide décrit un mouvement de va-et-
vient le long d’une paroi (figure 1), un processus thermoa-
coustique apparaît. D’abord, quand la particule est dans des
positions situées à gauche de sa position d’équilibre (figure
1), un transfert de chaleur allant du gaz vers la paroi appa-
raît, car la température de la particule de gaz s’est élevée
à une valeur supérieure à la température locale de la paroi
du fait de la compression quasi adiabatique imposée par
l’onde acoustique entretenue en cet endroit. De façon simi-
laire, au cours de la demi-alternance suivante, quand la parti-
cule est dans des positions situées à droite de sa position
d’équilibre (figure 1), un transfert de chaleur allant en sens
inverse (de la paroi vers le gaz) apparaît, car la tempéra-
ture de la particule de gaz se trouve abaissée à une valeur
inférieure à la température locale de la paroi du fait de la
détente quasi adiabatique imposée par l’onde acoustique
en cet endroit. De la sorte, au cours d’un cycle, la particule
de gaz assure le transport d’une petite quantité de chaleur
de la droite vers la gauche le long de la paroi (traduit dans
les équations de la chaleur par la dérivée temporelle parti-
culaire en représentation d’Euler) ; de la sorte un gradient
de température s’établit au cours du temps. C’est le proces-
sus qui est mis en œuvre dans un réfrigérateur thermoa-
coustique, l’énergie nécessaire à l’entretien du phénomène
provenant de la source du champ acoustique.
Si un gradient de température élevé est maintenu le long de
la paroi (par un couple de sources chaude et froide), les flux
de chaleur mentionnés ci-dessus sont inversés et la fonc-
tion de la «machine» est inversée : elle passe de la fonction
«réfrigérateur» (ou «pompe à chaleur») à la fonction «moteur»,
c’est-à-dire ici à la fonction «générateur» (création d’un champ
acoustique à partir d’énergie thermique). De l’énergie acous-
tique est créée du fait que la particule est détendue (augmen-
tation de son volume) globalement pendant une phase de
surpression (écart instantané de pression positif dû à l’ap-
port de chaleur provenant de la paroi) et comprimée (dimi-
nution de son volume) pendant une phase où l’écart instan-
tané de pression est négatif (dû au transfert de chaleur vers
la paroi). Pendant la première phase citée elle restitue donc
à son environnement plus d’énergie qu’elle en a accumulée
pendant la phase de compression qui précédait (il y a donc
création d’énergie acoustique à partir de l’énergie thermique
fournie par les sources qui maintiennent le gradient de tempé-
rature élevé le long du stack). Cet effet de génération d’un
champ acoustique à partir de sources de chaleur (quelle que
soit leur origine) peut être exploité pour alimenter en énergie
acoustique un réfrigérateur thermoacoustique.
→ →

