Version HTML de base


34
Caractérisation dynamique des matériaux et réduction des nuisances vibroacoustiques : l’apport des vibrations. Partie 1
Fig. 8 : Pendule de torsion –oscillation libre
Ecarté de sa position d’équilibre les oscillations du pendule
décroissent suivant des lois différentes en fonction du
mécanisme de dissipation.
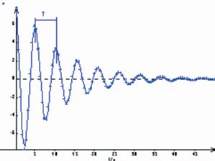
Par exemple pour un matériau viscoélastique on observe
une décroissance proportionnelle à la vitesse, figure 9 et
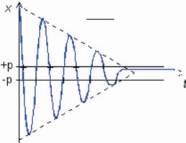
pour un frottement solide (ou frottement sec) une décrois-
sance indépendante de la vitesse, figure 10.
Fig. 9 : Frottement visqueux
Fig. 10 : Frottement sec
La mesure de la pulsation et du décrément logarithmi-
que permet de calculer les composantes réelle et imagi-
naire du module de cisaillement G du matériau. Dans ce
qui suit nous ne nous intéresserons qu’au pendule équi-
libré (masse du volant d’inertie et du mors équilibré), cf.
méthode B explicitée dans les normes.
G’ = 4
π
2
I (ƒ
d
2
F
d
-ƒ
0
2
)F
g
G’’ = 4
π
2
Iƒ
d
2
(
Λ
-
Λ
0
)F
g
Avec :
F
g
: facteur de correction égal à 3L/bh
3
F
c
pour une section
rectangulaire (cf. norme ISO 4664-2 & 6721-2 pour autres
sections) ;
F
c
: facteur de correction géométrique égal à 1-0,63h/b quand
0<h/b<0,6 et 0,843/(1+h
2
/b
2
) quand 0,6<h/b<1 ;
I : moment d’inertie du volant (kg.m
2
) ;
ƒ
d
: fréquence d’oscillation avec l’échantillon (Hz) ;
ƒ
0
: fréquence d’oscillation sans l’échantillon (Hz) ;
b, h, L : respectivement, largeur, épaisseur et longueur
entre mors de l’échantillon (m) ;
F
d
=1+
Λ
2
/4
π
2
: facteur de correction à prendre en compte
si
D
>1 et égal à 1 si
D
<1 ;
D
: Décrément logarithmique égal à ln(Xi/X
i+1
) avec X
i
et
X
i+1
amplitude de 2 oscillations consécutives (cf. norme
ISO 4664-2 & 6721-2)
La fréquence de sollicitation est comprise entre 0,1 Hz
et 10 Hz.
Documents de référence - Normes:
- ISO 4664-2 Rubber, vulcanized or thermoplastic –
Determination of dynamic properties – part 2: Torsion
pendulum methods at low frequencies.
- ISO 6721-2 Plastics – determination of dynamic mechani-
cal properties – part 2: Torsion-pendulum method.
Vibration forcée à la résonance
Contrairement à l’analyse d’un échantillon, comme dans
la plupart des méthodes que nous décrivons, la vibration
forcée à la résonance s’apparente à l’analyse modale d’une
structure plus ou moins complexe.
L’analyse modale est un outil efficace pour déterminer les
propriétés dynamiques d’un système mécanique au travers
de ses fréquences de résonance. (Fréquences propres,
modes propres et amortissements modaux).
Fig. 11 : Banc Oberst en étuve

