Version HTML de base

20
Spécial “ 5es Assises sonore ”
Acoustique
&
Techniques n° 51
Modélisation de la propagation acoustique en milieu extérieur complexe : Effets de frontière
Météo-BEM
On peut étendre l’application de la BEM à des cas d’atmosphère
inhomogène où le gradient vertical de vitesse du son est
constant. Dans ce cas météorologique particulier, deux
approches distinctes peuvent être menées : premièrement, on
peut appliquer le principe de transformée conforme et mener
un calcul BEM en atmosphère homogène mais en courbant le
sol (de façon concave ou convexe suivant le signe du gradient),
ce qui équivaut à une simulation en atmosphère inhomogène
à gradient constant mais sur sol non-courbé [5].
La seconde approche consiste à implémenter une BEM avec
une fonction de Green qui prend en compte le caractère
inhomogène du milieu de propagation, mais avec la contrainte
numérique de devoir être numériquement dérivable [6]. Deux
solutions implémentables (en fonction du signe du gradient)
sont les modes normaux et la série des résidus.
Méthode couplée BEM-PE
Une autre façon de mener des calculs à géométries complexes
avec prise en compte d’effetsmétéorologiques consiste à créer
une méthode hybride à partir de deux modèles distincts dédiés
chacun à une problématique de la propagation : la frontière
complexe et l’atmosphère inhomogène [7]. Une solution est
d’effectuer un couplage entre la BEM et l’équation parabolique,
méthode adaptée à la prise en compte des effets de gradient
vertical de vitesse du son et présentée en détail dans l’article
de Cotté et Blanc-Benon [1] du présent magazine.
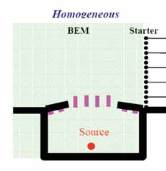
Un premier calcul est effectué en champ proche de la source
sonore en atmosphère homogène (voir, en Figure 2, le cas
d’une autoroute en tranchée avec semi-couverture ajourée)
afin de déterminer les caractéristiques du champ vertical initial
(«starter») pour le calcul en champ lointain de la propagation
en atmosphère inhomogène au-dessus d’une géométrie simple
(ici, terrain plat impédant).
Autres méthodes de références
Il existedenombreusesautresméthodes
dédiées à la prévision de la propagation
acoustique en milieu inhomogène [8]
mais pour des conditions relativement
simples de frontière (tel un sol plan
impédant) : le Fast Field Program, les
faisceaux gaussiens, les équations
d’Euler, l’équation parabolique… Nous
renvoyons ici le lecteur à l’article de
Cotté et Blanc-Benon [1] où certains
de ces modèles sont présentés.
Optimisations par
algorithme génétique
Principe
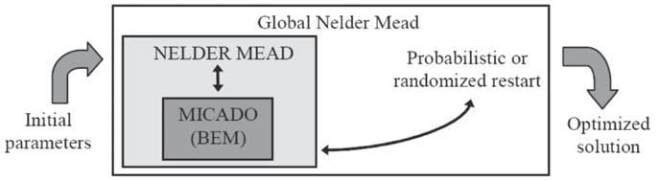
Il est nécessaire dans un premier
temps d’utiliser une méthode directe
d’optimisation adaptée à la recherche
locale. Le choix s’est porté sur la
méthode de Nelder Mead pour son
efficacité dans la détermination de
minimum locaux. Une globalisation de
l’optimisation peut ensuite être effectuée
par couplage avec une méthode
stochastique d’optimisation (Figure 3).
Fig. 2. : Principe de couplage entre la BEM et la PE
Fig. 3. : Principe de globalisation de l’optimisation
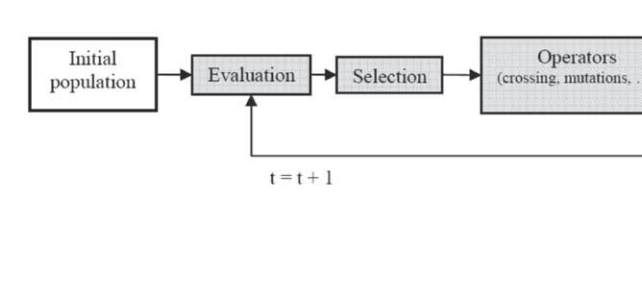
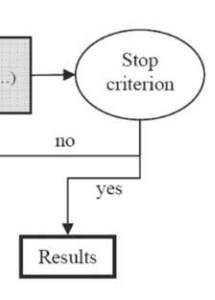
Fig. 4. : Principe d’un algorithme évolutionnaire

