Version HTML de base


Spécial “ CFM 2007 ”
7
Acoustique
&
Techniques n° 50
Modélisation de la propagation acoustique à moyenne distance du bruit des trains à grande vitesse
Chaque source est décrite par un spectre en tiers d’octave
du niveau de pression à 1 mètre, une directivité horizontale
et une directivité verticale. Les caractéristiques des sources
ont été obtenues à partir des résultats de différents projets,
parmi lesquels on peut citer le projet DEUFRAKO K2 (Talotte
et al., 2000 ; Mellet et al., 2006).
Au temps t au récepteur, le niveau de pression est obtenu en
sommant les contributions de chacune des sources
équivalentes
i
S
. Le niveau de pression pour la source
i
S
sur
le tiers d’octave (n) est calculé à l’aide des relations :
L
i
n
=
W
i
n
20 log
10
d
1,i
( )
+
A
e
( )
i
n
,
,
(2)
W
i
n
=
L
i,1m
n
V ,
i
(
)
+
D
i
n
,
,
(3)
où
W
i
n
est le terme source,
20 log
10
d
1,i
( )
correspond à
l’atténuation géométrique, avec d
1,i
la distance entre la source
et le récepteur, et
A
e
( )
i
n
est l’atténuation due à la propagation
du son dans l’atmosphère. La distance d
1,i
peut être exprimée
en fonction de la vitesse V, du temps au récepteur t et des
paramètres géométriques (voir par exemple Morse et Ingard
(1968)). Le terme source est calculé selon l’équation (3),
avec
L
i,1m
n
V ,
i
(
)
le niveau de pression à 1 mètre pour la
source S
i
corrigé par l’effet Doppler, et
D
i
n
la correction de
directivité. L’atténuation
A
e
( )
i
n
due aux effets de propagation
dans l’atmosphère est calculée avec un modèle analytique
qui prend en compte la réflexion d’une onde sphérique sur un
sol impédant et l’absorption atmosphérique (Chessel, 1977 ;
Salomons, 2001). Le calcul est réalisé sur les tiers d’octave
entre 50 et 5000 Hz.
Les résultats du modèle sont comparés aux mesures en
champ proche de la figure 1. La voie est posée sur une couche
de ballast de 75 cm épaisseur, qui repose elle-même sur un
remblai de 2,50 m de hauteur. Il est important de prendre
en compte cette géométrie pour calculer correctement
l’atténuation due à l’effet de sol. L’impédance du sol est
modélisée par le modèle phénoménologique de Hamet et
Bérengier à trois paramètres (Bérengier et al., 1997). Pour le
ballast, la résistivité au passage de l’air est 20 kN.s/m
4
et la
porosité est 0,6 ; pour le remblai et pour le sol, la résistivité
au passage de l’air est 100 kN.s/m
4
et la porosité est 0,4. La
tortuosité est 2,5 dans les deux cas. Les résultats du modèle
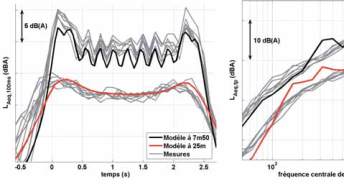
sont comparés aux mesures dans la figure 6. Les signatures
temporelles sont en bon accord, même si on remarque qu’il
y a un décalage au début des signatures à 25 m. Il existe
quelques différences entre les spectres de L
Aeq,tp
calculés
et mesurés, notamment sur les tiers d’octave entre 200
et 400 Hz. Par ailleurs, le modèle d’impédance de sol de
Delany-Bazley a été testé et permet également d’obtenir des
résultats satisfaisants. Les principales caractéristiques des
passages de TGV sont donc bien reproduites par le modèle.
Les différences observées entre résultats expérimentaux et
numériques peuvent provenir des modèles de source, en
particulier pour les sources aérodynamiques qui ne sont pas
parfaitement caractérisées.
Conclusions
Des résultats expérimentaux et numériques ont été présentés
afin d’identifier les principaux paramètres influant sur la
propagation acoustique du bruit des TGV. Des mesures
Fig. 5 : Modèle de 31 sources équivalentes pour le TGV.
Fig. 6 : Signatures temporelles (gauche) et spectres en tiers d’octave de L
Aeq,tp
(droite) mesurés et calculés à 7,50 m et 25 m de la voie.

