Version HTML de base



Spécial “ CFM 2007 ”
19
Acoustique
&
Techniques n° 50
Etude expérimentale du mécanisme d’excitation aéroacoustique des césures automobiles
d’onde. Ainsi, l’ensemble de l’excitation aéroacoustique
produite par l’écoulement au-dessus de la césure est modélisée
par un terme source qui s’exprime sous la forme d’une densité
autospectrale de puissance de pression
. Ce terme
source dépend de la DSP de l’excitation
et d’une
fonction , intégrale sur qui dépend des paramètres
aérodynamiques et acoustiques caractérisant la structure
spatiale de l’excitation au-dessus de la césure :
(1)
avec
Ce terme source vient exciter la cavité (point p sur la figure
13) qui se comporte alors comme un filtre fréquentiel
. Ce dernier terme peut dépendre de la vitesse de
l’écoulement amont
0
U
. Cependant, comme les vitesses sont
relativement faibles, l’impédance acoustique de l’ouverture
dépend faiblement de la vitesse de l’écoulement affleurant. Il
est alors possible d’exprimer la DSP dans la cavité de césure
selon la formule :
(iii) (ii)
(i)
Les termes (i) , (ii) et (iii) représentent les trois maillons du
modèle.
Validation du modèle
Afin de déterminer le maillon excitation du modèle, il est
nécessaire de déterminer la structure spatiale de l’excitation.
Pour cela, on se donne un modèle analytique qui dépend de
plusieurs paramètres. La part turbulente des fluctuations de
pression est modélisée à l’aide du modèle de Corcos ([3]),
modèle classique pour représenter les fluctuations de pression
créées par une couche limite turbulente. La part acoustique
est modélisée à partir d’un modèle de champ diffus. Les
paramètres caractéristiques de ce modèle sont recalés à
partir des mesures expérimentales de pression en paroi en
utilisant une procédure d’identification décrite dans [4].
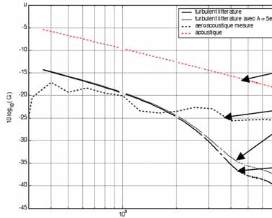
Il est alors possible de calculer la fonction , tracée en
figure 14. Les fluctuations de pression de nature purement
acoustique sont beaucoup moins atténuées que les
fluctuations de pression purement aérodynamique. Dans ce
dernier cas, il existe une fréquence de coupure à 2kHz environ
pour une longueur de césure de 10 mm. Pour une excitation
aéroacoustique d’amplitude acoustique non négligeable, la
part acoustique de l’excitation devient donc dominante à partir
de 2 kHz.
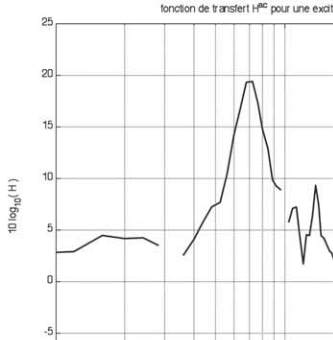
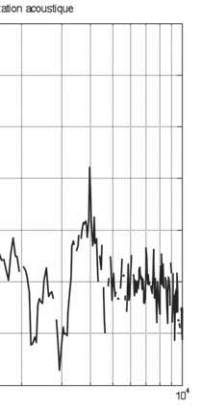
Pour déterminer le maillon filtrage fréquentiel
, figure
15, la mesure en salle réverbérante avec un champ diffus
acoustique est utilisée.
Fig. 14 : Fonction de filtrage spatial G(
ω
). Des objets ne peuvent pas être créés à partir des codes de champs de mise en forme.. Excitation
aérodynamique calculée à partir de paramètres classiques pour une couche limite turbulente, référence [3] (trait noir épais), excitation
aérodynamique avec paramètres classiques et excitation acoustique arbitraire (trait noir fin). Excitation aérodynamique et acoustique avec
paramètres issus de la mesure (trait noir pointillé). Excitation purement acoustique (trait pointillé rouge). Longueur de césure L = 10mm.
Fig. 15 : Fonction de filtrage fréquentiel H
c
(
ω
). Des objets ne peuvent
pas être créés à partir des codes de champs de mise en forme.
mesurée sous excitation champ diffus acoustique

