Version HTML de base

10
Spécial “ CFM 2007 ”
Acoustique
&
Techniques n° 50
Psychomécanique appliquée aux Trains à Grande Vitesse
La pression acoustique est ensuite déterminée par l’intégrale
de Kirchhoff-Helmholtz qui relie pression et déplacement.
Cette intégrale fait intervenir la fonction de Green de la cavité
; nous avons fait le choix d’utiliser une méthode d’images
pour la formuler. Le code de calcul correspondant à cette
théorie a été intitulé CaPrICe (Calcul de pression à l’intérieur
d’une cavité).
En considérant les résultats obtenus pour la plaque dans
l’air sans et avec la cavité, nous pouvons voir l’influence
de la cavité, notamment sur les fréquences des modes
de résonance. Comme on le retrouve souvent dans la
bibliographie - par exemple Dowell et al. (1977) – le premier
mode de la plaque est le mode principalement influencé par
la cavité car c’est un mode de «déplacement de volume».
Cependant l’influence de la cavité sur la première fréquence
de plaque n’est sensible que pour un coefficient de réflexion
b des parois supérieur à 0,5 (2% de variation pour b = 0, 5
et 6% de variation pour b = 1).
Afin de confronter les résultats obtenus avec l’expérience,
nous avons construit une cavité à cinq parois rigides en
matériau sandwich et fermée par une plaque mince en
aluminium. Le matériau sandwich est constitué de trois
couches : deux plaques de médium d’épaisseurs différentes
enserrant une couche d’élastomère. Une étude préliminaire
a montré l’efficacité d’un tel dispositif dont les vibrations
sont négligeables par rapport à celle de la plaque vibrante.
Les conditions aux limites d’encastrement de la plaque sont
réalisées en la serrant entre deux mâchoires dont une est
solidaire de la cavité. L’excitation est un bruit blanc produit par
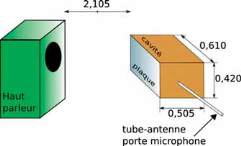
un haut-parleur faisant face à la plaque vibrante (cf. figure 1).
La pression est alors mesurée à l’intérieur de la cavité.
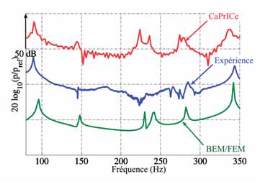
La figure 2 présente les spectres de pression obtenus
avec Caprice, avec l’expérimentation et avec une méthode
développée au Laboratoire de Mécanique et d’Acoustique,
utilisant des éléments finis et de frontière. On peut remarquer
que la même tendance est obtenue avec ces trois méthodes.
Cependant, la première fréquence de résonance expérimentale
de la plaque ne semble pas aussi élevée qu’on pourrait
l’espérer par les calculs. Ce phénomène peut s’expliquer
par les fuites acoustiques provoquées par les conditions aux
limites expérimentales de la plaque. Aussi, la méthode de
calcul de la fonction de Green pour un coefficient de réflexion
proche de 1 produit des artéfacts numériques en basses
fréquences. En effet, la mesure au tube de Kundt du coefficient
de réflexion des parois de la cavité expérimentale est de 0,98.
Ces artéfacts peuvent être supprimés en ajoutant un nombre
suffisant d’images au détriment du temps de calcul.
L’étude d’une voiture de TGV
en basses fréquences
Pour un TGV, la modélisation analytique est évidemment plus
complexe que pour le système plaque/cavité. Nous avons
donc décidé de caractériser le TGV expérimentalement grâce
à une analyse modale opérationnelle c’est-à-dire en condition
de roulement et sans connaissance a priori des sources
excitatrices. Les modes déterminés, dans la bande 0-200
Hz, sont alors uniquement les modes excités lorsque le train
roule. Outre la disponibilité d’un TGV vide de voyageur, une des
difficultés expérimentales est d’instrumenter la voiture avec
un nombre suffisant de capteurs acoustiques et vibratoires.
Fig 1 : Schéma et photographie de l’expérience réalisée
sur le système plaque/cavité (en chambre sourde).
Les dimensions indiquées sont en mètres
Fig. 2 : Spectres de pression obtenus avec Caprice, avec une
méthode couplée BEM/FEM et avec l’expérimentation.
Pour une meilleure comparaison visuelle, les courbes
sont volontairement espacées de 50 dB en ordonnée

