Version HTML de base
Spécial “ Acoustique sous-marine ”
61
Acoustique
&
Techniques n° 48
des conditions de continuité aux interfaces et
ε
n
est le
coefficient de Neumann (
ε
n
= 1 si n = 0 et
ε
n
= 2 si n
≠
0).
Une transformée de Fourier inverse est appliquée sur ce
spectre de rétrodiffusion. Sur le signal temporel obtenu,
l’écho spéculaire lié à la réflexion sur le tube est supprimé.
Sur le nouveau signal ainsi obtenu une transformée de
Fourier est appliquée permettant d’obtenir le spectre de
résonance. La méthode de calcul est comparable à la
MIIR développée pour l’expérimentation.
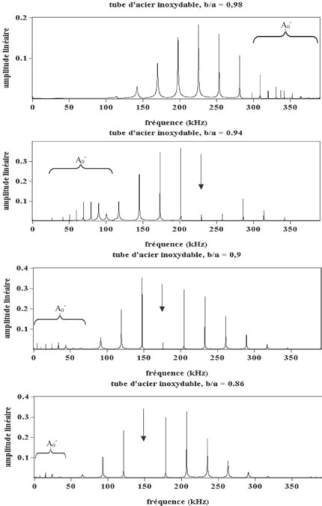
La figure 4 présente quelques exemples de calcul pour
des tubes ayant le même rayon extérieur (
a
= 3 cm) mais
différents rapports des rayons
b/a
(0,98, 0,94, 0,90 et
0,86).
Plusieurs remarques peuvent être faites :
- les résonances appartenant à l’onde
A
0
-
n’apparaissent
pas dans le même domaine de fréquence, plus la coque
est épaisse, plus cette bande glisse vers les basses
fréquences ;
- les autres résonances appartiennent à l’onde
S
0
. La
largeur des résonances n’est pas la même dans les 4 cas.
L’amplitude relative de ces résonances dépend également
du rapport des rayons, par exemple, il est possible de
constater qu’une résonance de très faible amplitude,
indiquée par une flèche sur la figure 4, est entourée de
résonances plus intenses. Cette résonance s’observe
au voisinage de la fréquence 230 kHz pour le tube
Fig. 4 : Spectres de résonance de tubes ayant différents rapports des rayons b/a
Diffusion acoustique par des cibles cylindriques : reconnaissance par signature spectrale

