Page 60 - base

Spécial “ Acoustique sous-marine ”59
Acoustique
&
Techniques n° 48
Diffusion acoustique par des cibles cylindriques : reconnaissance par signature spectrale
Il existe une infinité de ces ondes qui se différencient
essentiellement par leur structure vibratoire sur l’épaisseur.
Deux familles d’ondes de Lamb sont observables : les
ondes à vibration symétrique (Si) par rapport au plan moyen
de la plaque et les ondes à vibration antisymétrique (Ai), la
tôle se déforme comme un serpent. Les vitesses de ces
ondes, contrairement aux ondes de volume longitudinales
et transversales rencontrées dans les solides massifs
dépendent fortement de la fréquence, elles sont dites
dispersives. L’ensemble de ces ondes vont nous
permettre d’expliquer les résultats obtenus sur les tubes.
Pour comprendre complètement le comportement de ces
ondes dans une coque plongée dans l’eau, il faut savoir
qu’elles ont une polarisation de type elliptique, il existe
une composante vibratoire perpendiculaire à la surface et
une autre parallèle à la surface. Si la composante normale
à la surface est grande, des échanges importants
d’énergie se font entre le solide et le fluide, au contraire
si la composante parallèle est grande, elle se propage
avec peu d’échange et peut ainsi parcourir dans la coque
cylindrique un grand nombre de circonférences.
Dans une première partie, la Méthode d’Isolement et
d’Identification des Résonances impulsionnelle [4-6] est
décrite. Celle-ci permet d’obtenir expérimentalement
deux types de spectres acoustiques : le spectre de
rétrodiffusion et le spectre de résonance. Ces spectres
correspondent à la réponse vibratoire d’un tube
métallique, rempli d’air, plongé dans l’eau et excité
normalement à son axe par une impulsion ultrasonore
très brève. Dans une seconde partie, des spectres
calculés sont présentés montrant la possibilité de
reconnaissance de tubes. L’épaisseur de coque et la
constitution des tubes sont considérées. Enfin, dans une
dernière partie, une application de cette méthode est
développée pour détecter et reconnaître un tube enfoui
dans du sable très fin modélisant un sédiment.
Méthode d’Isolement et d’Identification des
Résonances : MIIR
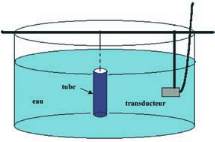
Le tube, de grande longueur devant les longueurs
d’ondes, est plongé verticalement dans une cuve remplie
d’eau douce (fig. 1) dans laquelle les ondes acoustiques
se propagent à la vitesse C eau = 1470 m/s.
Le tube est en acier inoxydable, son rayon externe est
a = 6 cm et le rapport des rayons interne b sur externe
a est b/a = 0,98. La vitesse de l’onde à vibration
longitudinale dans l’acier inoxydable est CL = 5970 m/
s et la vitesse de l’onde à vibration transversale est
CT = 3100 m/s. Ce tube est excité par une impulsion
acoustique brève émise par un transducteur large bande.
Le signal après diffusion par le tube est capté par le même
transducteur fonctionnant en récepteur et est transmis à
un micro-ordinateur afin d’être traité. La bande passante
de l’impulsion acoustique générée par le transducteur de
fréquence centrale 1 MHz est donnée sur la figure 2a.
Fig. 1 : Cuve d’expérimentation
Ondes de Lamb dans des plaques minces
Dans un matériau solide de grandes dimensions, deux types d’ondes de volume peuvent se propager de manière
indépendante : les ondes à vibration longitudinale et les ondes à vibration transversale (fig. 1), ces deux propagations
ne sont pas couplées. La vitesse de ces ondes de volume est indépendante de la fréquence. Dans un métal courant
comme l’acier ou l’aluminium, la vitesse des ondes à vibration longitudinale (Cl) est voisine de 6000 m/s et la
vitesse des ondes à vibration transversale (Ct) est voisine de 3000 m/s.
Dans une plaque plane de faible épaisseur, deux types d’ondes guidées peuvent se propager : les ondes de Lamb
Antisymétriques Ai et les ondes de Lamb symétriques Si (fig. 2). Dans chaque type, il en existe une infinité (i = 0,
1,2…), elles se différencient par la structure vibratoire dans l’épaisseur de la coque. Des flèches sur la figure 2
montrent d’une part la direction de propagation et d’autre part la direction des vibrations, dans le cas des ondes
de Lamb les vibrations sont elliptiques, les vibrations longitudinales et les vibrations transversales ne sont plus
indépendantes mais couplées. La vitesse de phase des ondes de Lamb dépend fortement de la fréquence comme
le montre la figure 3. Ces ondes sont dites dispersives, la fréquence réduite sur l’axe des abscisses est ktd avec
kt le nombre d’onde de l’onde à vibration transversale (kt = 2pF/Ct) et d la demie épaisseur de la plaque, pour
plus d’information vous pouvez consulter l’ouvrage de I. A. Viktorov (Rayleigh and Lamb Waves, Plenum Press,
New York, 1 967).