Version HTML de base
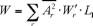
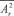
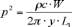
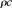
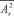
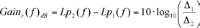
28
Acoustique
&
Techniques n° 46-47
le couplage du rail à l’ensemble de la plate-forme (traverse et
ballast), la raideur de la voie est déterminée par la raideur du
ballast et la raideur en flexion du rail.
Zone 2 :
F
ballast
< f < F
anti-résonance
, le taux de décroissance
chute par découplage du rail par rapport à l’ensemble de la
voie, il y a résonance du système «rail+traverse» sur la raideur
du ballast, on peut l’observer sur la courbe d’accélérance :
F
ballast
Les études paramétriques sous RODEL ont montré que
cette zone était pilotée principalement par l’amortissement
du ballast.
Zone 3 :
F
anti-résonance
< f < F
semelle
, le taux de décroissance
atteint sa valeur maximale. Ce phénomène traduit une anti-
résonance du rail et une résonance de la traverse dans laquelle
est transmise une grande partie de l’énergie excitatrice.
Cette anti-résonance est présente entre les 2 fréquences de
résonance F
semelle
et F
ballast
sur la courbe d’accélérance.
Les études paramétriques sous RODEL ont montré que cette
zone était pilotée par l’amortissement de la semelle sous
rail.
Zone 4 :
F
semelle
< f , les taux de décroissance s’effondrent à
partir de la fréquence de découplage rail-traverse. Les ondes
se propagent alors librement dans le rail. Leur atténuation
spatiale est uniquement provoquée par l’amortissement
intrinsèque du rail et par l’amortissement indirect issu des
attaches.
Les études paramétriques ont mis en évidence que les 2
facteurs, accélérance de la voie et taux de décroissance des
ondes dans le rail, sont liés. La détermination des fréquences
de résonance sur la courbe d’accélérance mesurée permet de
déterminer les valeurs de raideur de la semelle sous rail et du
ballast ainsi que la valeur de la masse sous traverse.
La même observation peut être menée dans la direction
latérale avec la courbe d’accélérance latérale.
La réponse vibratoire de la voie et le phénomène de propagation
des ondes dans le rail sont suffisamment représentés par la
formulation masse-ressort de type « RODEL » dans le domaine
fréquentiel inférieur à la fréquence propre du rail sur ses appuis
(traverses).
On peut maintenant relier le taux de décroissance aux niveaux
de bruit émis par la voie.
Impact des taux de décroissance sur le niveau de
bruit émis par la voie
Le lien [8] entre réponse vibratoire de la voie et rayonnement
acoustique est donné par l’expression de la puissance
acoustique totale rayonnée par le rail :
W’r représente la puissance acoustique (par mètre de rail)
rayonnée par l’onde r pour un déplacement unitaire du rail.
caractérise la réponse moyenne du rail suivant une force
d’excitation et en prenant en compte l’amplitude de la réponse
vibratoire de chaque type d’onde r.
L
1
est la longueur sur laquelle la moyenne est exprimée
(généralement la longueur du véhicule).
Pour obtenir l’expression de la pression acoustique, il
est maintenant nécessaire de s’imposer un modèle de
rayonnement, par exemple une source linéique monopolaire
pour l’onde de flexion verticale du rail (hypothèse TWINS).
On obtient ainsi la pression quadratique moyenne (Valeur RMS) :
Avec impédance acoustique de l’air et y la distance
source/observateur.
En remplaçant successivement Wpuis par leur expression,
il vient finalement la relation de la pression quadratique
moyenne en fonction du taux de décroissance de l’onde r
dans le rail : p
2
=f(
Δ
).
Et l’on en déduit l’influence d’une modification du taux de
décroissance de l’onde r sur le niveau de bruit qu’elle produit :
(1)
Cette relation (1) est potentiellement très robuste, car elle
est indépendante du modèle de rayonnement choisi et ne
repose finalement que sur la linéarité des phénomènes
de vibration et de rayonnement. Par contre, elle doit être
appliquée séparément pour chaque type d’onde, c’est-à-dire
pour l’onde verticale et pour l’onde latérale.
Résultats et applications
Impact du serrage des attaches de rail
sur le bruit émis
On a vu que les taux de décroissance s’effondraient à partir
de la fréquence de découplage rail-traverse : résonance du
rail seul sur la semelle sous rail, le rail étant alors découplé
de la traverse. Cette fréquence de résonance est directement
dépendante et pilotée par la raideur de la semelle sous rail :
plus la semelle va être raide, plus la fréquence de découplage
sera élevée et plus on maintiendra des taux de décroissance
élevés dans le domaine fréquentiel.
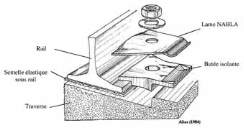
Au-delà de la raideur intrinsèque du matériau élastique de la
semelle sous rail, le serrage de l’attache de rail vient comprimer
(Figure 10) la semelle et conditionne donc la raideur globale
du système d’attache du rail sur la traverse. Plus l’attache va
être serrée, plus la semelle sous rail va être raide.
Fig. 10 : Système d’attache de la voie
Caractérisation vibro-acoustique
d’une voie ferrée
Approfondissons…

