Version HTML de base
18
8
e
CFA - Tours 2006
Acoustique
&
Techniques n° 45
pour interpréter ces phénomènes. À titre d’exemple,
on peut citer le comportement élastique typiquement
d’un bloc de roche soumis à une contrainte uniaxiale
lors d’expériences de compression quasi-statiques [1].
Il est dorénavant bien établi que la structure complexe
du matériau (inclusions souples dans une matrice dure)
est responsable de la réponse non linéaire. L’analogie
avec les microfissures dans les matériaux conduit au
phénomène similaire. En plus de la relation non linéaire,
nous discernons des comportements radicalement
différents durant les phénomènes de compression et de
dilatation : une dépendance en fonction de la compression
maximale lors des phases de dilatation, et un effet
mémoire via la dépendance en fonction de l’histoire de
la compression (compression précédente). Même si la
non-linéarité observée lors de l’expérience présentée en
Figure 1 concerne des niveaux de déformation importants,
l’hypothèse est également faite pour les non-linéarités
micromécaniques dans la relation contrainte-déformation.
celle-ci influence de façon drastique la réponse dynamique
du matériau soumis à des déformations bien plus faibles
en régime acoustique.
Par exemple, la distorsion de l’onde de déformation
au cours d’une propagation acoustique dans un milieu
non linéaire est illustrée en Figure 2. Chaque relation
contrainte-déformation non linéaire conduit à une relation
module-déformation dépendant de l’amplitude ; le module
étant calculé à partir de la dérivée de la contrainte par
rapport à la déformation. Dans cet exemple, le module
est plus faible pour des grandes valeurs d’amplitude de
déformation, alors qu’il est plus important pour de petites
amplitudes de déformation. Ceci implique que la célérité
des ondes acoustiques diminue lorsque les déformations
augmentent, conférant ainsi à la non-linéarité la propriété
de « ramollir » les matériaux.
Ainsi, durant la propagation, les surpressions vont se
propager moins vite que les dépressions. Ceci génère
alors une déformation de la forme d’onde, qui, si elle
est sinusoïdale, conduira à la création de nouvelles
composantes spectrales (les harmoniques) facilement
observables macroscopiquement. D’autres effets peuvent
également apparaître. La non-unicité de la relation
contrainte-déformation, matérialisée par un hystérésis,
conduit à une perte d’énergie, appelée extra-atténuation non
linéaire, produite lors de chaque cycle d’excitation
de la déformation. Les discontinuités dans la
relation module-déformation génèrent également
des phénomènes de génération d’harmoniques
ou des phénomènes plus complexes de mélange
de fréquences avec l’apparition de produits
d’intermodulation, etc.
Dans la recherche de nouvelles méthodes de
CND améliorées en sensibilité et susceptibles
de localiser et quantifier des dégradations
microstructurelles dans une large gamme de
matériaux, de nombreuses équipes de chercheurs
à travers le monde ont développé des techniques
innovantes qui explorent le comportement
micromécanique des matériaux et leurs effets
sur la propagation d’ondes acoustiques en
observant les propriétés macroscopiques et
leurs dépendances en fonction de l’amplitude [1-
19]. Ces méthodes sont appelées Spectroscopie
d’Ondes Élastiques Non Linéaires (NEWS pour
Nonlinear Elastic Wave Spectroscopy). L’objet
de ces méthodes est de mesurer et d’analyser
la signature macroscopique de la violation locale
de la relation linéaire contrainte-déformation à
l’échelle microscopique [1-3,19].
De nombreuses techniques NEWS ont été
développées pour montrer l’existence de la non-
linéarité induite par la dégradation des matériaux
(délaminations, microfissures, ou liaisons
adhésives fragilisées). Cette non-linéarité a été
observée en étudiant la génération d’harmoniques
et de produits d’intermodulation entre les
fréquencesacoustiquesd’excitation, lesdécalages
de fréquences de résonance avec de l’amplitude,
mais également en observant les contributions
non linéaires aux propriétés d’atténuation. Le
succès des méthodes NEWS appliquées au CND
s’explique par le fait que la dégradation interne
peut être mesurée via une détection instantanée
de l’augmentation du paramètre non linéaire.
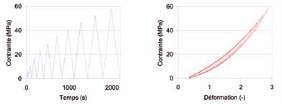
Fig. 1 : Exemple de comportement non linéaire dans les roches : visualisation
d’une expérience de compression uni-axiale quasi-statique d’un bloc
de Serena faisant apparaître une relation non linéaire et non-univoque
de la caractéristique contrainte-déformation, mettant en évidence des
effets de mémoire.
Gauche : protocole de compression.
Droite : mesure de la réponse contrainte-déformation
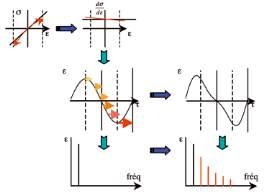
Fig. 2 : Un exemple de transformation non linéaire d’une onde.
La non-linéarité de la relation contrainte-déformation est
à l’origine de la dépendance de la célérité de l’onde en
fonction de l’amplitude, conduisant à la déformation du
profil de l’onde et à la génération d’harmoniques.
Détection et localisation de microdégradation de matériaux par spectroscopie d’ondes élastiques non linéaires

