Version HTML de base
8
e
CFA - Tours 2006
11
Acoustique
&
Techniques n° 45
zone f
11
- f
coin
, dite zone de loi de masse. Cette zone est
en majeure partie contrôlée par des modes non résonnants,
et par des modes en coïncidence spatiale dans une seule
direction [24] [25].
Deux enseignements à tirer de ce type d’études :
- un mode résonnant n’est pas obligatoirement rayonnant sauf
si k
mn
= k (coïncidence entre les nombres d’onde du mode
mn et du milieu récepteur).
- si l’excitation est riche dans la zone f
11
- f
coin
ou f
11
- f
c
,
augmenter l’amortissement structural sera donc peu efficace,
voire d’effet quasi nul.
On voit tout l’intérêt d’examiner les effets spatiaux caractérisant
l’excitation et non pas de raisonner uniquement en termes
de coïncidence fréquentielle. Attention à ce piège très
classique.
Comportement des cylindres de rayon a
Avec une excitation par onde plane repérée dans un plan
tangent au cylindre par
(θ,ψ)
et un milieu interne absorbant,
Cremer [26] (1955), obtient le facteur TL du cylindre de
longueur infinie et souligne deux comportements distincts :
- dans la zone 0-f
R
, décroissance du TL, minima très marqué
à la fréquence d’anneau f
R
: cette zone est gouvernée par des
effets d’extension de la coque et f
R
correspond au premier
mode de respiration (l’axe du cylindre ne bouge pas).
- pour f > 1,2 f
R
, on retrouve le comportement des plaques en
flexion car la longueur d’onde de vibration est petite devant
le rayon a.
Nous en restons là jusqu’en 1976 où Koval étudiant le même
objet excité par une onde d’incidence
θ
avec
ψ
= 0, met
en évidence deux singularités : f
R
, f
c
. Elle n’explique pas
physiquement la présence de f
c
et l’appelle fréquence critique
de plaque [27].
En 1990, nous reprenons le même cas avec une onde plane
(θ,ψ)
[28] et soulignons la présence de trois singularités : f
R
, f
pc
, (fréquence de coïncidence pseudo-critique) et f
coin
. Nous
montrons que f
pc
dépend de
θ
et
ψ
(ce qui n’est pas le cas
d’une plaque) et fournissons les explications physiques liées
à f
R
, f
pc
et f
coin
. En faisant varier le facteur de perte structural
η
s, nous montrons que la zone f
R
- f
pc
y est insensible car
gouvernée par des effets de coïncidence spatiale.
Arrêtons-nous un instant sur un autre «piège» vibroacoustique :
il est lié à la résolution numérique. L’onde plane incidente
développée en coordonnées cylindriques entraîne des
réponses vibratoires et acoustiques qui se présentent sous
la forme de séries d’ordre n (circonférentiel) de fonctions de
Bessel. L’interprétation de f
pc
(double coïncidence spatiale et
maximum de rayonnement) oblige pour une fréquence donnée
à sommer sur n jusqu’à :
n >
ω
/c . a cos
θ
;
ω
: est la pulsation – c : la célérité du
son
Pour des structures aéronautiques (type A320) ou spatiales
(Ariane 5), il faut aller jusqu’à n=20 à 1 000 Hz et n=120 à 10
000 Hz alors que l’obtention de la fréquence de coïncidence
nécessite n=2 à 3. C’est à partir du moment où nous avons
expliqué analytiquement la signification de f
pc
, que nous avons
pu rectifier l’erreur de Cremer et la nôtre (ref. [1], p.247).
Cette analyse permet aussi une stratégie intéressante.
Si l’on examine le comportement de coques orthotropes à
une couche ou multicouches (composites), on peut sachant
que l’on retrouve les trois singularités précitées, jouer sur le
rapport d’orthotropie pour rapprocher f
coin
de f
R
et avoir ainsi
au-delà de f
R
une croissance du TL en 18 dB/octave. C’est
cette stratégie que nous avons préconisée pour la future fusée
Ariane [29] [30] [31].
Il n’en reste pas moins que l’ennemi n°1 pour la transmission
du son par des cylindres reste la fréquence d’anneau f
R
qui dans le cas de structures finies, s’interprète comme la
fréquence d’accumulation des modes (n=0,m variable). Elle
se retrouve sur des systèmes bilobiques, sur des troncs de
cône (forme voisine d’un cockpit d’avion). Avec des méthodes
de contrôle actif, c’est elle qu’il faut viser en priorité.
Effets dus à l’excitation
Les champs excitateurs généralement étudiés en vibration sont
du type force et moment ponctuel ou forces delta-corrélés.
En acoustique, on examine l’effet d’ondes planes, sphériques,
cylindriques et de champ diffus : ce dernier est généralement
modélisé par une somme d’ondes planes indépendantes. En
fait, on peut montrer que la fonction de corrélation spatio-
fréquentielle entre deux points de ce champ est un sinus
cardinal. Dans la réalité, les excitations de pression pariétale
sont du type :
S
p
(M,M’,f) = S
p
(M,f) . R (M-M’,f)
S
p
(M,M’,f) désigne la densité interspectrale de
puissance, S
p
(M,f) la DSP locale, et R la fonction d’inter
corrélation spatio-fréquentielle.
1
ère
remarque : les excitations classiques utilisées en
vibrations ne portent aucune information spatiale, à
moins que l’on utilise deux forces avec contrôle de
phase et avec variation de la distance (M-M’).
2
ème
remarque : les recherches portant sur la réponse
vibroacoustique à des excitations du type couche
turbulente (CLT) établie sont peu nombreuses. Quelques
simulations ont cependant été réalisées.
Prenons deux cas :
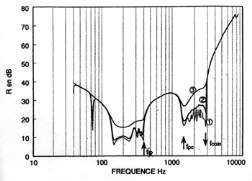
Fig. 1 : Indice d’affaiblissement acoustique d’un cylindre
θ
= 45°.
ψ
1
= 0.
Influence de l’amortissement structural :
(1)
η
s = 10
-3
; (2)
η
s = 10
-2
; (3)
η
s = 10
-1
. [28]
Vibroacoustique : Évolutions et perspectives

